命题与证明第11题答案
证明：（1）因为2是质数，但它是偶数，所以这个命题是假命题
（2）取a=45°，β=45°，则a+β= 90°，
所以α=β，且α，β 互余，
所以这个命题是假命题。
命题与证明第12题答案
解：∵DF⫽BC（已知），
∴∠1+∠2=180°（两直线平行，同旁内角互补）
∵∠1= 62°（已知），
∴∠2 =118°（等式性质），
又∵AB⫽DE（已知）
∴∠3=∠2（两直线平行，同位角相等）
∴∠3 =118°（等量代换）
命题与证明第13题答案
证明：过点E向左作EF⫽AB（图略），结合AB⫽CD，知EF⫽CD，
∴∠1=∠AEF，∠2=∠CEF（两直线平行，内错角相等）
∵∠AEC=∠AEF+∠CEF，
∴∠AEC=∠1+∠2（等量代换）
命题与证明第14题答案
（1）证明：如图D-13-1连接AC，
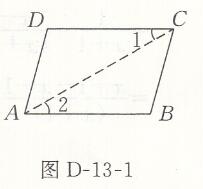
∵AB⫽CD（已知），
∴∠1=∠2（两直线平行，内错角相等）
∵∠DAB=∠BCD（已知），
∴∠DAB-∠2=∠BCD-∠1（等式性质）
即∠DAC=∠BCA，
∴AD⫽BC（内错角相等，两直线平行）
（2）解：成立
命题与证明第15题答案
解：（1）先利用活动角工具测量有关角的度数，再利用“同位角相等，两直线平行”或“同旁内角互补，两直线平行”检测a⫽b
（2）能。方法：先用没有刻度的直尺作过B、C两点的直线，再用活动角工具测量∠ABC与∠BCD的度数，然后利用“内错角相等，两直线平行”检测c⫽d 。（答案不唯一）
数学八年级上册轻轻松松学数学冀教版
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
浙教版八年级下册数学课本答案
八年级下册数学新编基础训练答案北师大版
人教版八年级下册生物知识与能力训练答案
八年级下册物理阳光学业评价答案人教版
八年级下册历史同步导学与优化训练答案人教版
生物八年级下册学习与评价答案苏科版
八年级下册生物长江作业本答案人教版
八年级下册历史南方新课堂答案人教版
八年级下册思想品德课时练答案人教版
人教版八年级上册生物知识与能力训练答案