相似三角形的性质第10题答案
证明：∵△ABC∽△DEF，
∴∠B=∠E，AB/DE=BC/EF，
又因为G，H分别为边BC和EF的中点，
∴BG=1/2BC，EH=1/2EF，
∴BG/EH=（1/2BC）/（1/2EF）=BC/EF，
∴BG/EH=AB/DE
由因为∠B=∠E
∴△ABG∽△DEH，
∴AG/DH=AB/DE=k
相似三角形的性质第11题答案
解：（1）设△ABC的周长为x cm，△EBD的周长为y cm
因为AB/EB=BC/BD=AC/ED=5/2
∴△ABC∽△EBD
又相似比为5/2，由题意得
∴△ABC的周长为100 cm，△EBD的周长为40 cm
（2）设△ABC的的面积为a cm2，△EBD的面积为b cm2
由题意得
∴△ABC的的面积为700 cm2，△EBD的面积为112 cm2
相似三角形的性质第12题答案
证明：∵DC∥AB
∴△DOC∽△BOA
∴OC:OA=OD：OB
又∵AD∥BE，∴△ODA∽△OBE，
∴OA:OE=OD:OB
∴OC:OA=OA:OE，即OA2=OC·OE
相似三角形的性质第13题答案
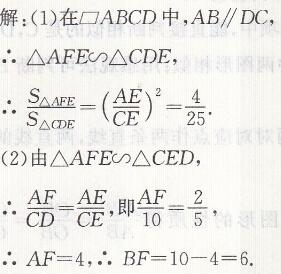
相似三角形的性质第14题答案
解：∵AD∥BC，∴△ADE∽△BCE，
∴S△ADE：S△BCE=AE2：BE2
又∵AE:BE=1：2
∴S△ADE：S△BCE=1:4
∵S△ADE=1，∴S△BCE=4
∵EF∥BC，∴△AEF∽△ABC，
∴EF:BC=AE:AB
∵AE:EB=1：2，
∴EF:BC=AE:BE=1：3，
又∵△ADE∽△BCE，
∴AD:BC=AE:BE=1：2，BC=2AD
∴EF:AD=2：3，
∵AD∥EF，∴△ADE与△AEF等高
∴S△AEF：S△ADE=EF:AD=2:3
∵S△ADE=1，∴S△AEF=2/3
相似三角形的性质第15题答案
解：由AB=1.5米，S△ABC=1.5平方米，得BC=2米，
若设甲加工的桌面边长为x米，由DE∥AB，
推出Rt△CDE∽Rt△CBA，
可求出x=6/7
设乙加工的桌面边长为y米，
过点B作Rt△ABC斜边AC上的高BH，交DE于点P，交AC于点H
由AB=1.5米，BC=2米，S△ABC=1.5平方米，
得AC=2.5米，BH=1.2米
∵DE∥AC，∴Rt△BDE∽Rt△BAC，
∴BP/BH=DE/AC，即（1.2-y）/1.2=y/2.5，
解得y=30/37
∵6/7=30/35＞30/37，即x＞y，x2＞y2
∴甲同学的加工方法符合要求。
数学九年级上册轻轻松松学数学冀教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级上册语文同步训练答案人教版
九年级上册数学同步解析与测评答案人教版
人教版九年级上册历史知识与能力训练答案
人教版九年级下册语文南方新课堂答案
九年级下册化学新编基础训练答案人教版
九年级下册化学同步解析与测评答案人教版
九年级下册化学同步练习答案沪教版
译林牛津版九年级下册英语课本答案
九年级下册数学补充习题答案苏科版
人教版九年级下册数学作业本答案江西省