相似三角形的判定第12题答案
解：（1）△AQP∽△APB∽△PRB
（2）因为△AQP∽△PRB，所以AQ/PR=PQ/BR，
即PR·PQ=AQ·BR，
而PR=PQ=QR，
所以QR2=AQ·BR
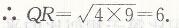
相似三角形的判定第13题答案
解：图中与△ADE相似的三角形有△CDA，△BAE
理由：在△ADE和△CDA中，
∵∠ADE=∠CDA，∠DAE=∠C=45°，
∴△ADE∽△CDA
同理，可得△ADE∽△BAE
相似三角形的判定第14题答案
证明：设AB=BE=EF=FC=a，因为∠B=90°，
所以由勾股定理得AE=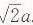
，
又因为
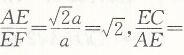
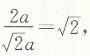
所以AE/EF=EC/AE，而∠AEF=∠CEA，
所以△AEF∽△CEA
相似三角形的判定第15题答案
分析：（1）由矩形BDEF知S1=1/2BD·DE=1/2EF·DE =1/2FC·DE+1/2 CE·DE=1/2 FC·BF+1/2 CE·DE=S2+S3
（2）△BCF∽△DBC∽△CDE，证明两个三角形相似，利用“两个角对应相等的两个三角形相似”进行证明。
解：（1）=
（2）△BCF∽△DBC∽△CDE
选△BCF∽△CDE，证明如下：
在矩形ABCD中，∠BCD=90°，
又点C在边EF上，
∴∠BCF+∠DCE=90°，
在矩形BDEF中，∠F=∠E=90°，
∴∠CBF+∠BCF=90°，
∴∠CBF=∠DCE，
∴△BCF∽△CDE
相似三角形的判定第16题答案
证明：（1）在△BEC和△ADC中，
∠CBE=∠CAD，∠BCE=∠ACD，
∴△BEC∽△ADC
（2）由△BEC∽△ADC，知CD/AC=CE/BC，
即CD·BC=AC·CE
∵AB=AC，∠ADB=90°，
∴BD=DC，∴CD=1/2BC
又∵AB=AC，
∴CD·BC=AC·CE，即为1/2 BC·BC=AB·CE，
即BC2=2AB·CE
数学九年级上册轻轻松松学数学冀教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级下册历史新编基础训练答案人教版
九年级上册语文同步练习答案苏教版
人教版九年级上册语文作业本答案江西省
苏教版九年级下册语文课本答案
人教版九年级英语南方新课堂答案
人教版九年级上册语文知识与能力训练答案
九年级上册语文课课练答案苏教版
数学九年级下册学习与评价答案苏科版
沪教版英语书九年级下册答案
人教版九年级上册语文新课程自主学习与测评答案