相似三角形第12题答案
解：因为∠C=90°，又因为∠BDC=30°，
所以∠DBC=60°
因为△ABD∽△BCD
所以∠A=∠DBC=60°
∠ABD=∠BCD=90°，∠ADB=∠BDC=30°
所以∠A=60°，∠ABC=90°+60°=150°，
∠C=90°，∠CDA=30°+30°=60°
相似三角形第13题答案
解：设△A'B'C'中最小边长为x，另一边长为y，
由题意得5/x=12/y=13/26，
解得x=10，y=24，
所以周长为10+24+26=60
因为52+122=132，
故△ABC是直角三角形，其中最大的角是直角，即90°的角，
而△A'B'C'∽△ABC，所以△A'B'C'中的最大角是直角。
答：△A'B'C'的另两边长分别为10,24，周长为60，最大角是90°。
相似三角形第14题答案
解：（1）因为DE∥BC，所以△ABC∽△ADE，
所以∠AED=∠ACB=40°，∠ADE=∠ABC（相似三角形对应角相等）
因为∠BAC+∠ACB+∠ABC=180°
所以∠ABC=180°-40°-45°=95°
所以∠ADE=95°
（2）因为△ABC∽△ADE，所以AE/AC=DE/BC，即5/8=DE/7，
所以DE=35/8
相似三角形第15题答案
解：当以30 cm的钢筋作最长边时，设其余两边的长分别为x cm，y cm，
由相似三角形的对应边成比例，得40/x=100/y=120/30，
所以x=10，y=25
当以30 cm的钢筋作次长边时，设另两边的长分别为x cm，y cm，
则有40/x=100/30=120/y，
所以有x=12，y=36，
故有两种不同的截法。
相似三角形第16题答案
解：因为四边形ABCD为平行四边形，
所以AD=BC，BC∥AD，DC∥AB
由BC∥DE，DF∥AB，可得△BFC∽△EBA∽△EFD，
得CF/BC=DF/ED=AB/EA，
所以CF/AB=BC/EA=AD/AE=
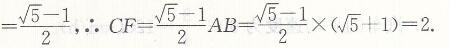
数学九年级上册轻轻松松学数学冀教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级下册数学书答案人教版
九年级下册英语新编基础训练答案译林版
九年级下册历史同步解析与测评答案人教版
九年级下册化学课本答案人教版
九年级下册历史新编基础训练答案北师大版
九年级下册语文课时练答案人教版
九年级上册语文同步解析与测评答案人教版
九年级下册语文同步练习答案苏教版
译林版英语书九年级下册答案