习题24.2第11题答案
解：相等。
理由如下：过O1作O1E⊥AB，垂足为E，02F⊥CD，垂足为F
∵∠O1EM=∠O2FM，∠O1ME=∠O2MF，OlM=O2M
∴△MO1E≌△MO2F，
∴OlE=O2F
又∴⊙Ol与⊙O2为等圆，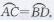
习题24.2第12题答案
解：连接CD。在Rt△ABC中，
∵∠C=90°，
∴∠A=90°-∠B=65°，
在△CAD中，
∵CD= CA，
∴∠CDA=∠A=65°，
∴∠DCA= 180°-(∠A+∠CDA)
=180°-(65°+65°)=50°
即
所对的圆心角为50°
习题24.2第13题答案
已知：如图24-2-73所示，AB为⊙O任意一条不是直径的弦，求证：直径是圆中最长的弦
证明：连接OA、OB，在△AOB中，OA+OB>AB，而OA+OB即为⊙O的直径的长，
∴直径是圆中最长的弦
解：不一定，一般的菱形的四个顶点到其中心的距离不相等，如果在同一个圆上，则该菱形为正方形。
习题24.2第15题答案
解：在轮片的圆弧上任取三点A、B、C，分别作线段AB、BC的垂直平分线，交点为O，则点O即为圆心，OA（或OB、OC）为半径。
习题24.2第16题答案
（1）已知：△ABC，求证：△ABC中至多只能有一个角是直角，
证明：假设△ABC中至少有两个直角，不妨设∠A=90°，∠B=90°
因此有∠A+∠B+∠C=90°+90°+∠C=180°+∠C>180°，
这与“三角形内角和等于180°”相矛盾，假设不成立。
所以△ABC中至多只能有一个直角
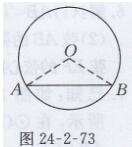
（2）已知：如图24-2-74所示，AB、CD是⊙O的两条弦，且AB≠CD，OE⊥AB于点E，OF⊥CD于点F，求证：OE≠OF
证明：假设OE=OF，连接OA、OD
∵OE⊥AB，OF⊥CD
∴∠OFD=∠OEA=90°，OA=OD,
∴Rt△OFD≌RtAOEA，
∴AE=DF
又∵AE=1/2AB，DF=1/2CD，
∴AB=CD，这与AB≠CD矛盾，故在同一个圆中，如果两条弦不相等，那么它们的弦心距也不等。
习题24.2第17题答案
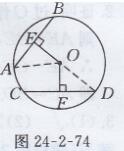
已知：如图24-2-75所示，两条直线AB、CD分别与直线EF平行， 即AB//EF，CD// EF
求证：AB//CD
证明：假设AB与CD不平行，则AB与CD相交，设AB与CD交于点G
由已知条件AB//EF，CD// EF得知，过点G有两条直线与直线EF平行，这与“经过直线外一点，有且只有一条直线平行于这条直线”相矛盾
所以，“假设AB与CD不平行”不成立，故AB//CD
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级物理新编基础训练补充习题答案人教版
九年级上册语文学法大视野答案人教版
人教版九年级上册数学课时练答案
九年级下册思想品德作业本答案人教版
九年级下册科学作业本答案浙教版
北师大版九年级下册数学作业本答案江西省
九年级下册英语同步解析与测评答案人教版
九年级下册数学新编基础训练答案人教版
九年级下册化学课时练答案人教版