习题24.2第1题答案
解：点B在⊙A上，C、D两点均在⊙A外，点M在⊙A上。
习题24.2第2题答案
已知：如图24-2-71所示，在菱形ABCD中，M、N、G、H分别为AB、BC、CD、DA边上的中点，求证：M、N、G、H在同一圆上。
证明：连接AC、BD交于点0，连接OM、ON、OG、OH
∵四边形ABCD为菱形，
∴AC⊥BD，AB=BC=CD=AD
在Rt△AOB中，
∵M为AB中点，
∴OM=1/2AB
同理OH=1/2AD，OG=1/2CD, ON=1/2BC
∴OM=ON=0G=0H
∴M、N、G、H均在以0为圆心，以OM为半径的圆上
习题24.2第3题答案
解：连接OA，过点O作弦AB的垂线，交AB于点M，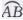
于点C，
由垂径定理得点M是AB的中点，点C是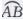
的中点，
且AM=1/2AB=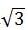
（cm）
在Rt△OAM中，由勾股定理， 得
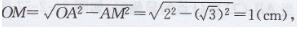
所以MC=OC-OM= 2-1=1(cm)，
即弦AB中点到它所对劣弧中点的距离为1（cm）
习题24.2第4题答案
提示：连接OA，过点A作OA的垂线交圆于点C、D，弦CD即为所求。
习题24.2第5题答案
提示：连接AB，作AB的垂直平分线l，与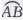
交于点C，点C即为所求的点。
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级物理新编基础训练补充习题答案人教版
九年级上册语文学法大视野答案人教版
人教版九年级上册数学课时练答案
九年级下册思想品德作业本答案人教版
九年级下册科学作业本答案浙教版
北师大版九年级下册数学作业本答案江西省
九年级下册英语同步解析与测评答案人教版
九年级下册数学新编基础训练答案人教版
九年级下册化学课时练答案人教版