答案网 - 课本习题,辅导练习，辅导材料等答案解析！
语文 数学 英语
书通网logo
当前位置: 书通网 > 答案 > 九年级配套练习册答案 > 九年级上册数学配套练习册答案人教版 >

人教版九年级上册数学22.1.3二次函数y=a（x-h）2+k的图像和性质第1课时配套练习册答案(2)

时间:2016-08-17 来源:书通网

第1课时第7题答案

（1）抛物线与x轴的交点 y=0，则0=-x2+4，解得x=±2，则坐标（-2，0）和（2，0） 

（2）当-2<x<2，y>0，当x<-2且x>2，y<0

第1课时第8~10题答案

8910
C
DB

第1课时第11题答案

（1）将原点（0，0）代入抛物线方程，得2m－m2=0，解得m=0或2 

（2）由顶点坐标（0，2m-m2）得2m-m2=-3，解得m=3或-1

第1课时第12题答案

把（1，-4）代入y=ax2-2得a-2=-4，

解得a=-2，

所以二次函数解析式为y=-2x2-2； 

当y=0时，-2x2-2=0，即x2+1=0，方程无实数解，

所以二次函数的图象与x轴的没有交点，函数的最大值为-2。

第1课时第13题答案

2.jpg

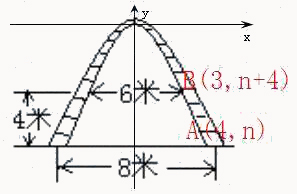
设二次函数的解析式是y=ax2， 点A的坐标是（4，n），点B的坐标是（3，n+4） 

将点A（4，n）、B（3，n+4）代入，得 

16a=n

9a=n+4

解得：a=-4/7，n=-64/7

∴该二次函数的解析式是y=（-4/7）x2， 

点A的坐标是（4，-64/7），则校门的高是64/7≈9.1米。

九年级上册数学配套练习册答案人教版

更多

推荐阅读

点击查看更多内容
优美的诗句 伤感的句子 好词好句 唯美的句子 思念的诗句 经典语句

声明 :本网站尊重并保护知识产权，根据《信息网络传播权保护条例》，如果我们转载的作品侵犯了您的权利,请在一个月内通知我们，我们会及时删除。

皖ICP备11009057号