函数单调性的运算性质

若函数f(x)，g(x)在区间I上具有单调性，则在区间，上具有以下性质：

(1) f(x)与f(x)+c（c为常数）具有相同的单调性．

(2) f(x)与a · f(x)在a>0时具有相同的单调性，在a<0时具有相反的单调性．

(3)若函数f(x)是增函数，函数g(x)是增函数，则f(x) + g(x)是增函数；

若函数f(x)是减函数，函数g(x)是减函数，则f(x) + g(x)是减函数；

若函数f(x)是增函数，函数g(x)是减函数，则f(x) - g(x)是增函数；

若函数f(x)是减函数，函数g(x)是增函数，则f(x) - g(x)是减函数．

(4)当f(x)恒不为0时，函数f(x)与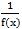单调性相反．

(5)当f(x)非负时，f(x)与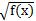具有楣同的单调性．

(6)当f(x)，g(x)都是增（减）函数时，若两者都恒大于零，则f(x)·g(x)也是增（减）函数；若两者都恒小于零，则f(x)·g(x)是减（增）函数．

(7) f(g(x))的单调性遵循“同增异减”的原则．