运用速度分解模型解题的基本规律

1．速度分解应遵循的原则

速度分解是运动分解的一部分，因此，速度分解应遵循的原则与运动分解应遵循的原则相同，具体内容如下：

 (1)应遵循矢量运算法则；

 (2)要按实际运动效果去分解；

 (3)分解的两个分速度应具有独立性；

 (4)分解应遵循有用原则，即分解后应有利于解题（使解题更简便、能与题目中的已知量或待求量联系起来）．

2．速度分解的两种基本模型

 (1)小船渡河模型

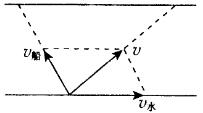
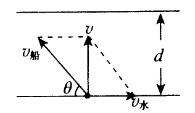
船横渡过河时，船的实际运动ν（即相对于河岸的运动）可以看成是随水以速度ν_水漂流的运动和以速度ν_船相对于静水的划行运动的合运动，这两个分运动互不干扰而且具有等时性，如图所示．

①渡河时间t最短问题

a．渡河时间t的大小取决于河岸的宽度d及船在垂直河岸方向上的速度的大小．

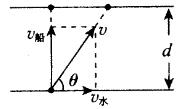
b．若要渡河时间最短，只要使船头垂直于河岸航行即可．由图可知，此时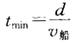，船渡河的位移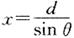，位移方向满足.    

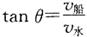②渡河位移最短问题

求解渡河位移最短问题，分为两种情况：

a．若ν_水﹤ν_船，最短的位移为河宽d，此时渡河所用时间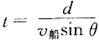，船头与上游夹角满足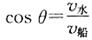，如图所示．

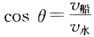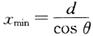b．若ν_水﹥ν_船，这时无论船头指向什么方向，都无法使船垂直河岸渡河，即最短位移不可能等于河宽d，寻找最短位移的方法是：按水流速度和船的静水速度大小的比例，先从出发点A开始做矢量ν_水，再以ν_水末端为圆心，以ν_船大小为半径画圆弧，自出发点A向圆弧做切线，其方向为船位移最小时的合运动的方向．这时船头与河岸夹角θ满足，最短位移，过河时间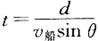，如图所示．

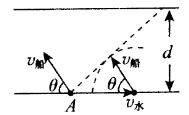
(2)绳端速度分解模型

沿绳的方向和垂直于绳的方向将绳端速度进行分解，这是分析绳端速度分解问题的一个关键，绳端的运动可以看成沿绳方向的运动和绕滑轮进行转动的合运动，绕滑轮转动耐，转动分速度与半径垂直，这一问题将在圆周运动中说明.