作业题第1题答案
(1)b：c=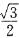
.
(2)∵
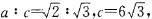
∴a=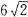
.
∴b=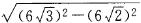
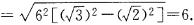
作业题第2题答案
解：由勾股定理得底边上的高h=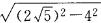
=2，
∴
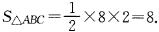
作业题第3题答案
解：由题意知EF=CD=30 m，CF=DE=50 m.
∴由迎水坡AD与背水坡BC的坡比，得AE=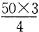
=37.50(m)，BF=100 m，
∴AB=AE+EF+BF=37.50+30+100=167.50(m)．
又AD=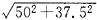
=62.50(m)，BC=
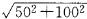≈111.80(m)，
∴周长为AB+BC+CD+DA≈371.80(m)，
面积为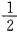
(CD＋AB)·DE=
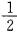×(30＋167.50)×50=4937.50(
).
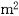点拨：利用条件求出AE和BF的长是关键．
作业题第4题答案
解：由题意知△AOB为等腰直角三角形．设OA=x，则OB=x，AB=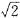
x．
∴2x＋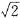
x=1×60，
∴
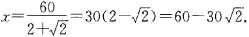
∴AB=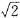
x=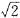
×(60-30
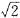)=60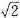
-60≈24.9(km).
答：A，B之间的距离约为24.9 km.
点拨：明确本题所走的路线是等腰直角三角形是解题关键．
作业题第5题答案
解：比较如图所示的甲、乙两种剪法，设AC=BC=a.
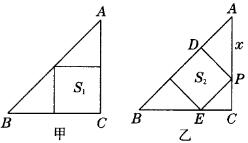
如图甲所示，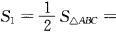
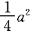；如图乙所示，设AP=x，则PD=PE，即
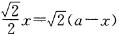，解得x=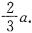
∴
∴
．
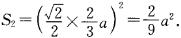
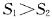∴用如图甲所示的剪法所得的正方形面积最大．如果这张纸板的斜边长为30 cm．则AC=BC=15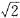
cm，S=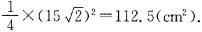
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册地理南方新课堂答案人教版
八年级上册语文同步练习答案苏教版
八年级下册英语同步训练答案人教版
八年级下册历史与社会作业本答案人教版
八年级下册地理同步导学与优化训练答案人教版
八年级上册译林版英语同步练习答案
八年级上册数学人教版长江全能学案答案
河北少儿版八年级下册生物作业本答案江西省
八年级下册地理新课程自主学习与测评答案人教版