拓展探究第1题答案
（1）（x+0. 7）2+22 =2.52 0.8 -2.2（舍去） 0.8
（2）①不会是0.9米②有可能，
设梯子顶端从A处下滑x米，
则有（x+0.7）2+（2.4-x）2=2.5 2，
解得x=1.7或x=0（舍去）
拓展探究第2题答案
（1）①设剪掉的正方形的边长为x cm，
则（40 – 2x）2=484，
解得x₁=31（不合题意，舍去），x₂=9，
∴剪掉的正方形的边长为9 cm
②侧面积有最大值，设剪掉的小正方形的边长为x cm，
盒子的侧面积为4（40-2x）x，
即-8（x-10）2+800，
∴当1=10时，即当剪掉的正方形的边长为10cm时，长方形盒子的侧面积最大为800 cm2
（2）在如图的一种剪裁图中，设剪掉的长方形盒子的高为x cm
2（40 -2x）（20-x） +2x（ 20-x）+2x（40- 2x）=550，
解得x₁= -35（不合题意，舍去），x₂=15
∴剪掉的正方形的边长为15 cm，此时长方体盒子的长为15 cm，宽为10 cm，高为5 cm
拓展探究第3题答案
（1）当t=4时，l=1/2×42+3/2×4=14（cm）
答：甲运动4s后的路程是14 cm
（2）设它们运动了m s后第一次相遇，根据题意，得
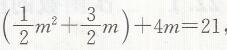
解得m1=3，m2=-14（不合题意，舍去），
答：甲、乙从开始运动到第一次相遇时，它们运动了3 s
（3）设它们运动了n s后第二次相遇，
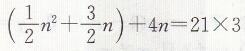
解得n1=7，n2=-18（不合题意，舍去），
答：甲、乙从开始运动到第二次相遇时，它们运动了7 s
拓展探究第4题答案
（1）设2012年甲校响应本校倡议的人数为x人，乙校响应本校倡议的人数为y人，
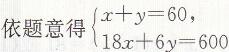
解得x=20,y=40
∴2012年甲、乙两校应倡议的人数分别是20人和40人
（2）设2012年到2014年，甲校响应本校倡议的人数每年增加m人；乙校响应本校倡议的人数每年增长的百分率为n
依题意得
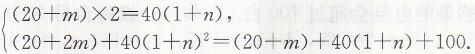
由①得m=20n，代入②并整理得2n2+3n-5=0，
解之得n₁=1，n₂=2.5（负值舍去）
∴m=20，
∴2014年两校响应本校倡议减排二氧化碳的总量：（20+2×20）×18+40（1+1）2×6=2040（千克）
答：2014年两校响应本校倡议减排二氧化碳的总量为2040千克。
九年级上册化学阳光学业评价答案人教版
九年级上册数学阳光学业评价答案人教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级下册数学课时练答案人教版
九年级下册语文课时作业本答案人教版
苏科版九年级上册数学补充习题答案
人教版九年级上册思想品德长江作业本答案
九年级上册物理配套练习册答案人教版
九年级下册物理课时作业本答案人教版
九年级上册历史学法大视野答案人教版
九年级下册数学同步解析与测评答案人教版
九年级下册数学书答案人教版
人教版九年级下册物理作业本答案江西省