第1章自测题第22题答案
（1）b=-15/8，c=59/2
（2）y=-（1/8）x2+（3/2）x+13/2
（3）4月份，最大利润为21/2元
第1章自测题第23题答案
（1）由OC=0.6，AC=0.6，得点A的坐标为（0.6，0.6），
代入y=ax2得a=5/3，
∴抛物线的解析式为y=（5/3）x2
（2）可设右边的两个立柱分别为C₁D₁，D₂C₂，
则D₁，D₂的横坐标分别为0.2，0.4 代入y=（5/3）x2，
得D₁，D₂的纵坐标分别为： y₁=5/3×0.22≈0.07，y₂=5/3×0.42≈0.27
∴立柱C₁D₁=0.6-0.07=0.53，C₂D₂=0.6-0.27=0.33
由抛物线关于y轴对称，栅栏所需立柱的总长度为：
2（C₁D₁+C₂D₂）+OC=2×（0.53+0.33）+0.6≈2.3米
第1章自测题第24题答案
（1）抛物线解析式为y=2/3·（x-7/2）2-25/6，顶点为（7/2，-25/6）
（2）S=2S三角形OAE=1/2 ×2×OA·|y|=-6y=-4×（x-7/2）2+25
自变量x的取值范围是1<x<6
①点E₁（3，-4）满足OE=AE，所以□OEAF是菱形；
点E₂（4，-4）不满足OE=AE，所以□OEAF不是菱形。
②当OA⊥EF，且OA=EF时，□OEAF是正方形，此时点E的坐标只能是（3，-3）
而坐标为（3，-3）的点不在抛物线上，故不存在这样的点E，使□OEAF为正方形
第1章自测题第25题答案
（1）当x=1或3米时，矩形框架ABCD的面积为3平方米，
（2）当x=3/2时，矩形架ABCD的面积S最大，最大面积是3平方米
（3）当x=a/（2n）时，矩形ABCD的面积S最大，最大面积是a2/(12n)立方米
第1章自测题第26题答案
（1）设抛物线的解析式为：y₁=a（x-1）2+4，
把A（3，0）代入解析式，求得a=-1
所以y₁=-（x-1）2+4=-x2+2x+3.
设直线AB的解析式为：y₂=kx+b，
由y₁=-x2+2x+3，求得点B的坐标为（0,3）
把A（3,0），B（0,3）代入y₂=kx+b中，
解得k=-1，b=3，所以y₂=-x+3
（2）因为点C的坐标为（1，4），
所以当x=1时，y₁=4，y₂=2，
所以CD=4-2=2 ，
S三角形CAB=1/2 ×3×2=3
（3）假设存在符合条件的点P，设点P的横坐标为x，∆PAB的铅垂高为h，
则h=y₁-y₂=（-x2+2x+3）-（-x+3）=-x2+3x
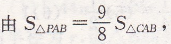得
1/2 ×3 ×（-x2+3x）=9/8 ×3
化简得4x2-12x+9=0，解得x=3/2
将x=3/2代入y₁=-x2+2x+3中，
解得点P的坐标为（3/2，15/4）
浙教版九年级上册科学课时特训答案
浙教版九年级上册数学课时特训答案
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级下册化学课时练答案人教版
九年级下册历史与社会作业本答案人教版
九年级下册英语新编基础训练答案外研版
人教版九年级上册语文作业本答案江西省
九年级下册数学书答案华东师大版
九年级上册语文配套练习册答案人教版
数学九年级上册学习与评价答案苏科版
九年级上册数学配套练习册答案人教版
九年级上册化学阳光学业评价答案人教版