思路探究例1答案
（1）在三角形中，一个角的平分线与它的对边相交，这个角的顶点与交点之间的线段就是三角形的角平分线
（2）用刻度尺量出AC的长度，取其长度的一半处便是边AC的中点
（3）外部，因为在△ABC中，∠C是钝角
解：如答图11.1.2 -5
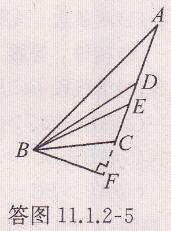
（1）BE为∠ABC的平分线，可表示为∠ABE = ∠CBE = 1/2∠ABC
（2）BD为边AC上的中线，可表示为AD = CD = 1/2AC
（3）BF为边AC上的高，可表示为BF⊥AC，∠F = 90°
思路探究例2答案
S△BEC S△CDE S△ABD S△ACD S△ACD S△ABC
解：因为点D是边BC的中点，所以△ABD和△ACD为两个等底同高的三角形，
所以S△ABD = S△ACD = 1/2S△ABC = 1/2 × 8 = 4（cm2）
同理，S△ABD = 1/2S△ABD = 2（cm2），S△CDE = 1/2S△ACD = 1/2 × 4 = 2（cm2）
所以S△BEC = S△BDE + S△CDE = 2 + 2 = 4（cm2），
又因为点F是边CE的中点，所以S阴影 = 1/2S△BEC = 1/2 × 4 = 2（cm2），
即阴影部分的面积为2 cm2。
针对训练第1题答案
D
针对训练第2题答案
B
达标检测第1题答案
B
达标检测第2题答案
C
达标检测第3题答案
40°
达标检测第4题答案
解：因为BE，CF分别为边AC，AB上的中线，且交于点O，
所以AB = 2AF = 2 × 6 = 12（cm），AC = 2AE = 2 × 4 = 8（cm），
且AD是△ABC的边BC上的中线，
所以BD = 1/2BC
又因为△ABC的周长为36 cm，
所以BC = 36 - 12 - 8 = 16（cm）
所以BD = 1/2 × 16 = 8（cm）
人教版八年级上册数学课时练答案
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
八年级下册英语阳光学业评价答案沪教版
八年级上册物理课堂精练答案北师大版
八年级下册物理长江全能学案同步练习册答案人教版
苏教版八年级下册语文课本答案
数学八年级下册学习与评价答案苏科版
八年级下册数学课课练答案苏科版
人教版八年级上册英语长江作业本答案
苏教版八年级上册生物补充习题答案
八年级下册数学课时特训答案浙教版
人教版八年级上册英语作业本答案