能力展示第2题答案
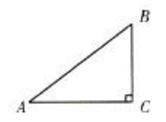
在 Rt△ABC中，∠C=90°
∴tanA=BC/AC=3/4
∴设BC=3k, AC=4k
∵BC2 + AC2 = AB2 ,
∴（3k）2+（4k）2=52
∴k=1
∴BC=3，AC=4
∴sinA=BC/AB=3/5,cosB=BC/AB=3/5,tanB=AC/BC=4/3
尝试提高第1题答案
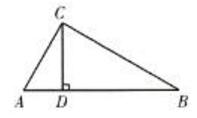
(1)∵∠ACB= 900，CD⊥AB于点D
∠A+∠B=90°
∠BCD+∠B=90°
∴∠A=∠BCD
(2) tanA=CD/AD=4/2=2
(3)∵∠A=∠BCD, tanA=2，tan∠BCD=BD/CD
∴BD/4=2.
∴BD=8
尝试提高第2题答案
∵CD⊥AB, AB为直径
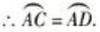
∴∠ABD = ∠ABC.∠ACB =90°
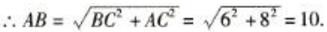
∴ cos ∠ABD = cos∠ABC =BC/AB = 6/10 =3/5
推荐阅读
人教版九年级英语南方新课堂答案
年级：九年级
版本：人教版
科目：英语
学期：下册
名称：南方新课堂
人教版九年级下册历史南方新课堂答案
年级：九年级
版本：人教版
科目：历史
学期：下册
名称：南方新课堂
人教版九年级下册语文南方新课堂答案
年级：九年级
版本：人教版
科目：语文
学期：下册
名称：南方新课堂
人教版九年级下册数学南方新课堂答案
年级：九年级
版本：人教版
科目：数学
学期：下册
名称：南方新课堂
鲁教版语文书九年级下册答案
年级：九年级
版本：鲁教版
科目：语文
学期：下册
名称：课本
北师大版数学书九年级下册答案
年级：九年级
版本：北师大版
科目：数学
学期：下册
名称：课本
人教版语文书九年级下册答案五四制
年级：九年级
版本：人教版
科目：语文
学期：下册
名称：课本
华东师大版数学书九年级下册答案
年级：九年级
版本：华东师大版
科目：数学
学期：下册
名称：课本
苏科版数学书九年级下册答案
年级：九年级
版本：苏科版
科目：数学
学期：下册
名称：课本
湘教版数学书九年级下册答案
年级：九年级
版本：湘教版
科目：数学
学期：下册
名称：课本
鲁教版数学书九年级下册答案五四制
年级：九年级
版本：鲁教版
科目：数学
学期：下册
名称：课本
译林版英语书九年级下册答案
年级：九年级
版本：译林版
科目：英语
学期：下册
名称：课本
沪教版英语书九年级下册答案
年级：九年级
版本：沪教版
科目：英语
学期：下册
名称：课本
外研版英语书九年级下册答案
年级：九年级
版本：外研版
科目：英语
学期：下册
名称：课本
九年级下册英语作业本答案人教版
年级：九年级
版本：人教版
科目：英语
学期：下册
名称：作业本
九年级下册历史同步解析与测评答案人教版
年级：九年级
版本：人教版
科目：历史
学期：下册
名称：同步解析与测评
浙教版九年级上册科学作业本答案
年级：九年级
版本：浙教版
科目：科学
学期：上册
名称：作业本
人教版九年级上册数学新课程自主学习与测评答案
年级：九年级
版本：人教版
科目：数学
学期：上册
名称：新课程自主学习与测评
湘教版数学书九年级下册答案
年级：九年级
版本：湘教版
科目：数学
学期：下册
名称：课本
九年级下册英语长江作业本答案人教版
年级：九年级
版本：人教版
科目：英语
学期：下册
名称：长江作业本
九年级下册化学课时练答案人教版
年级：九年级
版本：人教版
科目：化学
学期：下册
名称：课时练
九年级下册历史新课程自主学习与测评答案人教版
年级：九年级
版本：人教版
科目：历史
学期：下册
名称：新课程自主学习与测评
苏科版九年级上册数学伴你学答案
年级：九年级
版本：苏科版
科目：数学
学期：上册
名称：伴你学
九年级下册历史与社会作业本答案人教版
年级：九年级
版本：人教版
科目：历史
学期：下册
名称：作业本