第十八章综合练习（一）第一题答案
| 1 | 2 | 3 | 4 | 5 | 6 |
| D | B | C | C | A | B |
第十八章综合练习（一）第二题答案
7、略（答案不唯一）
8、=
9、略（答案不唯一）
10、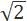
-1
第十八章综合练习（一）第三题答案
11、证明：∵四边形ABCD是平行四边形
∴OD=OB，OA=OC
∵AB∥CD
∴∠DFO=∠BEO，∠FDO=∠EBO
∴△FDO≌△EBO
∴OF=OE
∴四边形AECF是平行四边形
12、四边形OCED是矩形，理由：
∵DE∥AC，CE∥BD
∴四边形OCFD是平行四边形
∵四边形ABCD是菱形
∴AC⊥BD
∴∠DOC=90°
∴四边形OCED是矩形
13、四边形AEMF是正方形，理由：如下图所示：
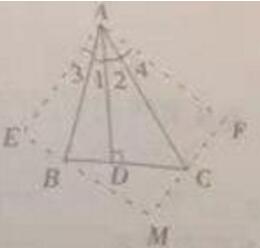
∵AD⊥BC，而△AEB由△ADB折叠所得
∴∠1=∠3，∠E=∠ADB=90°，BE=DE，AE=AD
又∵△AFC是由△ADC折叠所得
∴∠2=∠4，∠F=∠ADC=90°，FC=CD，AF=AD
∴AE=AF
又∵∠1+∠2=45°
∴∠3+∠4=45°
∴∠EAF=90°
∴四边形AEMF是正方形
14、（1）证明：∵DF垂直平分BC
∴DF⊥BC，DB=DC
∴∠FDB=∠ACB=90°
∴DF∥AC
∴E为AB的中点
∴CE=AE=1/2AB
∴∠FDB=∠ECA
又∵AF=CE=AE
∴∠F=∠AEF=∠EAC=∠ECA
∴△ACE≌△EFA
∴AC=EF
∴四边形ACEF是平行四边形
（2）∠B=30°，理由略
（3）四边形ACEF不可能为正方形，理由如下：
∵E为AB的中点
∴CE在△ABC内部
∴∠ACE＜∠ACB=90°
∴四边形ACEF不可能是正方形
人教版八年级下册数学配套练习册答案
人教版八年级下册物理配套练习册答案
八年级下册英语配套练习册答案人教版
八年级下册语文配套练习册答案人教版
八年级下册数学配套练习册答案青岛版
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册历史与社会思想品德课时特训答案人教版
苏科版八年级上册数学补充习题答案
八年级上册地理阳光学业评价答案人教版
八年级下册英语阳光学业评价答案沪教版
八年级上册语文同步练习答案苏教版
八年级下册数学书答案青岛版
八年级下册数学新编基础训练答案北师大版
人教版八年级上册语文书答案
八年级下册地理长江全能学案同步练习册答案人教版
八年级下册历史南方新课堂答案人教版