第七章复习题第7题答案
解：如下图所示：
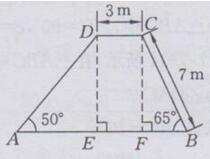
过点D、C分别作底边AB的垂线交AB于E、F两点，则DE⊥AB，CF⊥AB
在Rt△CFB中,BC=7 m，∠FBC=65°
∴CF=BC·sin∠FBC=7×sin65°≈6.34（m），BF=BC·cos∠FBC=7×cos 65°≈2.96(m)
∵CD∥AB，四边形DEFC为矩形
∴DE=CF=6.34 m，DC=EF=3 m
在Rt△AED中，∠DAE=50°，DE=6.34 m
AE=DE/(tan50°)=6.34/(tan50°) ≈5.32(m)
∴ AB=AE+EF+BF=5.32+3+2. 96≈11. 3(m)
答：坝高约为6.3m，坝底宽约为11.3m
第七章复习题第8题答案
解：如下图所示：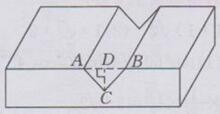
AB=30 mm，CD=12 mm
AD=1/2 AB=1/2×30=15(mm)
∴tan∠ACD=AD/CD=15/12
∴∠ACD≈51.34°
∴∠ACB=2∠ACD≈102.7°
答：v形角∠ACB的大小约为102.7°
第七章复习题第9题答案
解：如下图所示：
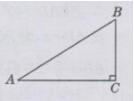
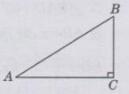
AB=8 m，BC=4.2 m，由三角函数的定义得：
sin∠BAC=BC/AB=4.2/8=21/40
∴∠BAC≈31.7°
答：自动扶梯倾斜角∠BAC的大小约为31.7°
第七章复习题第10题答案
解：如下图所示：
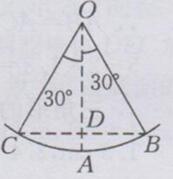
连接BC与OA，相交于点D，由题意知∠BOD=30°，OB=3m，OA⊥BC
∴OD=OB·cos 30°=3×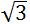
/2≈2.598(m)
∴AD=OA-OD≈3-2.598≈0.4（m）
答：最高位置与最低位置的高度差约为0.4m
第七章复习题第11题答案
解：如下图所示：
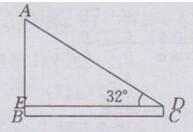
由题意知ED=45 m，∠ADE=32°，CD=1.2 m
AE=ED·tan 32°=45×tan 32°
∴AB=AE+BE=45×tan32°+CD=45×tan32°+1.2≈29.3m
第七章复习题第12题答案
解：如下图所示：
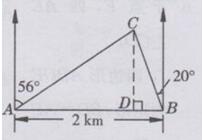
过点C作CD⊥AB于点D，则CD即为船C离海岸线的距离，设CD =x km
在Rt△ACD中，tan∠CAD=CD/AD，则AD= CD/(tan∠CAD)=x/(tan34°)
在Rt△BCD中，tan∠CBD=CD/BD，则BD=CD/(tan∠CBD)=x/(tan70°)
∵AB=AD+BD，AB=2 km
∴x/(tan34°)+x/(tan70°)=2
整理，得（tan 70°+tan 34°）x=2tan 34°·tan 70°
解得x≈1.1
所以CD=1.1 km
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
沪粤版物理书九年级下册答案
九年级上册思想品德学法大视野答案人教版
九年级下册数学长江作业本答案人教版
九年级上册思想品德课课练答案苏人版
九年级下册化学书答案鲁教版
人教版九年级下册英语作业本答案江西省
数学九年级上册轻轻松松学数学冀教版
九年级上册语文配套练习册答案人教版
九年级下册物理课本答案人教版
九年级下册数学作业本答案浙教版