习题7.6第1题答案
解：如下图所示：
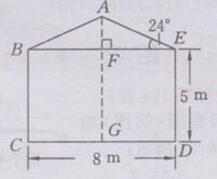
由题意知：CD=8 m，DE=5 m，∠AEB=24°，△ABE为等腰三角形，四边形BCDE为矩形
过点A作CD的垂线交BE于点F，交CD于点G，由等腰三角形的性质得：
BF= EF=1/2×8=4(m)
在Rt△AFE中
∵tan 24°=AF/EF
∴AF=EF·tan 24°
∴AG=AF+FG=AF+DE
=EF·tan 24°+5
=4×tan 24°+5
≈6. 8(m)
答：屋顶相对于地面的高度约为6.8m
习题7.6第2题答案
解：如下图所示：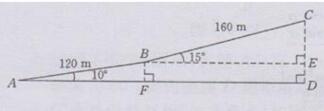
过点B作BE⊥CD交CD于点E,过点B作BF⊥AD交AD于点F
由题意知AB=120 m， BC=160m
∠BAF=10°，∠CBE=15°
在Rt△BFA中
∵sin∠BAF=BF/AB
∴BF=AB·sin∠BAF=120×sin10°
∵BF⊥AD，CD⊥AD，BE⊥CD
∴四边形BFDE为矩形
∴DE=BF
在Rt△BEC中
∵sin∠CBE=CE/BC
∴CE=BC·sin∠CBE=160×sin15°
∴CD=CE+ED=160×sin15°+120×sin10°≈62. 2(m)
答：小明沿垂直方向升高了约62.2m
习题7.6第3题答案
解：根据题意可知∠ABH =90°，∠BAH=35°，AB=20cm，AC=1.6m
在Rt△ABH中
tan∠HAB=HB/AB
所以HB=AB·tan∠HAB=HB/AB
所以树的高度为HD=HB+BD=20×tan35°+1.6≈15.6（m）
答：树的高度为15.6m
习题7.6第4题答案
解：如下图所示：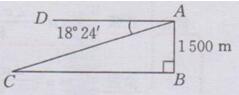
根据题意知：AB=1500m，∠DAC=∠C=18°24′
在Rt△ABC中
∵sinC=AB/AC
∴AC=AB/sinC=1500/(sin18°24')≈4752（m）
答：飞机到控制点的距离约为4752m
习题7.6第5题答案
解：如下图所示：
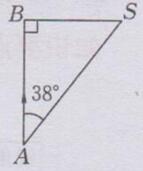
AB=15km，∠BAS=38°
在Rt△ABS中,tan38°=BS/AB
∴BS=AB·tan38°=15×tan38°≈11.7(km)
答：灯塔S与B处的距离约为11.7 km
习题7.6第6题答案
解：根据题意可知，∠TBC=28°，∠TAC=15°，TC=120m
在Rt△BCT中
∵tan 28°=TC/BC
∴BC=TC/(tan28°) =120/(tan28°)≈225.69(m)
在Rt△TAC中
∵tan15°=TC/AC
∴AC=TC/(tan15°)=120/(tan15°) ≈447.85(m)
∴ AB=BC+AC≈225.69+447.85≈673.5(m)
答：A、B两点的距离约为673.5m
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册数学课课练答案苏科版
苏科版九年级上册数学书答案
九年级上册数学配套练习册答案青岛版
教科版九年级下册物理作业本答案江西省
九年级上册数学课课练答案苏科版
苏人版九年级上册思想品德伴你学答案
九年级上册语文学法大视野答案北师大版
九年级下册英语同步练习答案译林版
九年级下册语文课时特训答案人教版