第三章复习题第27题答案
解：如下图所示：
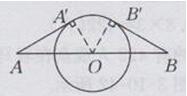
连接OA′，OB′
∵AA'切⊙O于点A'，BB'切⊙O于点B'
∴OA'⊥ AA'，OB'⊥BB'
∵AB=40 km
∴ BO=AO=1/2×40=20（km）
在 Rt △AO·sin 60°=20×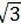
/2 =10 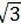(km)
同理∠BOB'=60°，BB'=10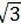 km
∴∠A'OB'=60°
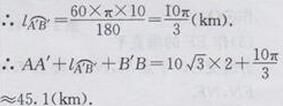
第三章复习题第28题答案
解：如下图所示：
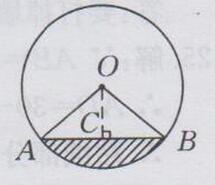
过点O作OC⊥AB于点C，
∴AC=1/2AB=1/2×30=15（m）
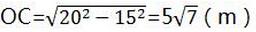
sin∠COA=AC/AO=15/20=0.75
∴∠COA≈48.59°
∴∠AOB≈97.18°
答：大约有422人观众在看马戏
第三章复习题第29题答案
解：如下图所示：
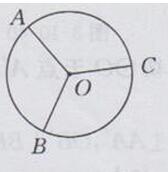
方案：
（1）确定圆心O；
（2）作一个120°的圆心角∠AOB
（3）以AB为半径，以B为圆心作弧交⊙O于点C.则OA，OB，OC将圆三等分
第三章复习题第30题答案
解：如下图所示：
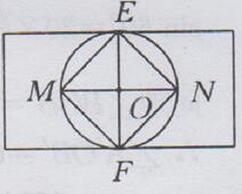
方案：
（1）作矩形一边的垂直平分线交两边于E，F两点
（2）以EF为直径作⊙O
（3）作EF的垂直平分线交00于点M，N，连接EM，MF，FN，NE
第三章复习题第31题答案
（1）如下图所示：
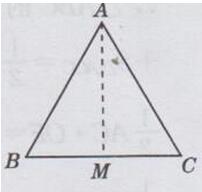
过点A作AM⊥BC，交BC于点M，将50m的篱笆设计成一个正三角形
则其边长为50/3m，则AB=BC=CA=50/3m，∠BAC=60°，则∠MAC =25/3
在Rt△AMC中
∵AM2=AC2-MC2
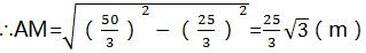
∴S△ABC=1/2 BC·AM
=1/2×50/3×（25/3 ）≈120.28（m2）
（2）将50米的篱笆设计成正方形，则其边长为50/4m=25/2m，
∴其面积S=（25/2）2=625/4=156.25（m2）
（3）如图3-10-45所示
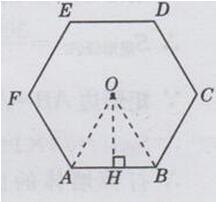
将50m的篱笆设计成正六边形ABCDEF，设正六边形ABCDEF的中心为点O
连接OA，OB，则其边长为50/6=25/3（m）
过点O作OH⊥AB于点H
则OH=OA·sin60°=25/3×/2=25/6 （m）
∴正六边形的面积ABCDEF的面积S1=6S△OAB =6×1/2×25/3×25/6≈180.42（m2）
（4）将50m的篱笆做成圆形，设圆的半径为r m，则2πr=50
∴r=50/2π=25/π，
此时圆的面积S2=π× 625/π2=625/π≈198.94（m2）
综上可知，圆形场地的面积最大
第三章复习题第32题答案
解：如下图所示：
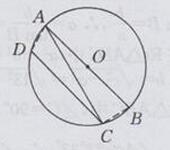
连接AD，BC
∵AB是⊙O的直径
∴∠ACB=90°
在Rt△ABC中
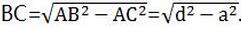
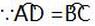
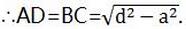
第三章复习题第33题答案
解：如下图所示：
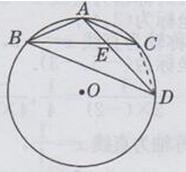
连接CD
∵AB=AC
∴∠ADC=∠ACE
又∵∠CAD=∠EAC
∴△AEC∽△ACD
∴AC/AD=AE/AC，即AC2=AD ·AE
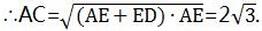
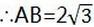
第三章复习题第34题答案
解：如下图所示：
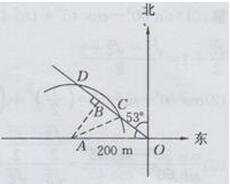
过点A作AB⊥OB于点B，则AB=OAsin（90°-53°）≈200×0.6018=120.36<130
∴学校A会受到货车影响
以点A为圆心，130m为半径作弧交射线OB于点C，D，连接AC
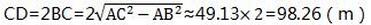
∴噪声污染时间=CD/5=98.26/5≈19.65≈20s
第三章复习题第35题答案
解：由题意知AH=BH
∴HC=500-BH
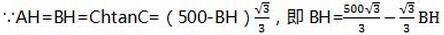
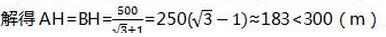
∴该公路弧穿过该森林公园
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
教科版物理书九年级下册答案
九年级下册语文作业本答案人教版
北师大版九年级上册数学书答案
九年级上册物理同步练习答案苏科版
九年级下册语文新课程自主学习与测评答案人教版
九年级下册数学补充习题答案苏科版
九年级上册语文同步解析与测评答案人教版
苏人版九年级上册思想品德伴你学答案
九年级下册数学书答案华东师大版
九年级下册英语课课练答案译林版