第三章复习题第17题答案
解：如下图所示：
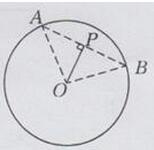
过点P作弦AB⊥OP，连接OA，OB
则∠AOB=2∠AOP
∵cos∠AOP=OP/OA=2/4=1/2
∴∠AOP=60°
∴∠AOB=120°
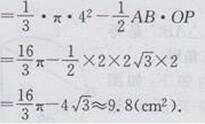
第三章复习题第18题答案
（1）∵⊙O的直径为2，PA=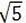
，
又∵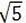>2，点A在⊙O上
∴点P一定在⊙O外
（2）∵⊙O的直径为2，PA=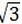
又∵2>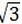
∴点P与⊙O的位置有两种情况：点P可能在⊙O内，也有可能在⊙O外
第三章复习题第19题答案
解：⊙P运动一圈与△OBC的边相切6次.第一次的相切是⊙P和OC相切
设切点为M，则PM⊥OC，且PM=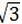
在Rt△PMO中，
∵PM=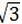，∠O=60°
∴PO=PM/(sin60°) =2
即第一次相切PO=2
则第二次与BC相切，PB=2
第三次和OB相切，PB=2
第四次和OC相切，PC=2
第五次和BC相切，PC=2
第六次和OB相切，PO=2
第三章复习题第20题答案
（1）如下图所示：
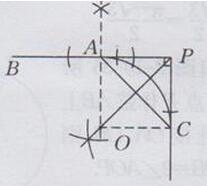
作法：
①作∠P的平分线PO
②过点A作AO⊥PB交PO于点O
③以点O为圆心，OA为半径作弧AC为所求
（2）如图3-10 -37所示，连接OC，得正方形AOCP
第三章复习题第21题答案
解：如下图所示：
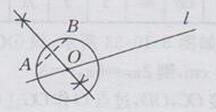
作法：
①作AB的垂直平分线交直线l于点D．
②以点O为圆心，以OA为半径作圆，则⊙O即为所求
（1）因为当直线l与AB不垂直时，AB的垂直平分线和直线l有唯一交点，即圆心，所以只可作一个圆
（2）当直线l与AB垂直但不经过AB的中点时，AB的垂直平分线必和直线l平行，即没有交点，无圆心，所以不能作圆
（3）当直线l是线段AB的垂直平分线时，圆心在直线，上的任何位置都可以，所以可作无数个圆
第三章复习题第22题答案
解：如下图所示：
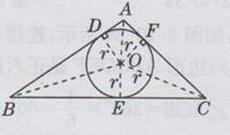
连接OA，OB，OC，设△ABC的内切圆切AB边于点D，切BC边于点E，切AC边于点F
连接OD，OE，OF，则OD=OE-OF=r
∴△ABC的面积S=S△AOB+ S△BOC+S△AOC
=1/2AB·OD+ 1/2BC·OE十1/2AC·OF
=1/2（AB+BC+AC）·r
=1/2l·r
第三章复习题第23题答案
在圆形纸片上，任作出两条互不平行的弦，并作出这两条弦的垂直平分线，两者的交点即为圆形纸片的圆心，量出这一点到圆上任一点的长，即为该圆形纸片的半径
第三章复习题第24题答案
解法1：连接BD，BC，BD交AC于点O，则点O为矩形ABCD外接圆的圆心，⊙O的半径为AC/2=2/2=1m
∵BO=CO=B C=1 m,
∴∠BOC= 60°
∴扇形OBAC的圆心角为300°
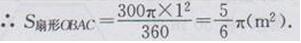
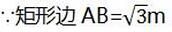
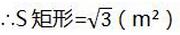
答：要打掉墙体的面积约为1.3m2
第三章复习题第25题答案
∵AB=30cm，BD=20cm
∴AD=30-20=10（cm）
第三章复习题第26题答案
解：这一比赛的危险区域的面积至少应为：
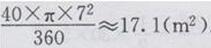
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
教科版物理书九年级下册答案
九年级下册语文作业本答案人教版
北师大版九年级上册数学书答案
九年级上册物理同步练习答案苏科版
九年级下册语文新课程自主学习与测评答案人教版
九年级下册数学补充习题答案苏科版
九年级上册语文同步解析与测评答案人教版
苏人版九年级上册思想品德伴你学答案
九年级下册数学书答案华东师大版
九年级下册英语课课练答案译林版