第三章复习题第1题答案
图（4）
第三章复习题第2题答案
解：如下图所示：
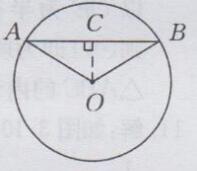
过点O作OC⊥AB于点C
∵OA =OB
∴∠AOC=∠BOC=1/2×120°-60°
在 Rt △AOC中 ,OC = AO·cos ∠AOC= 20 ×cos 60° = 20×1/2 =10（ cm）
AC=AO·sin 60°=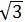
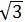20×/2=10（cm）
∴S△AOB=1/2 AB·OC=1/2×2×10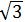
×10=100
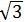（cm2）
第三章复习题第3题答案
解：如下图所示：
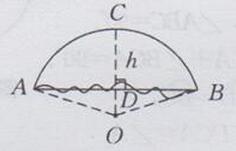
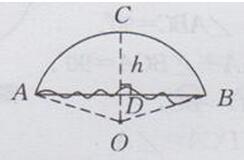
假设圆心为点O，过点0作OC⊥AB，OC交AB于点D，交弧AB于点C，则点C为弧AB的中点
∴ CD=h=0.25m
设车轮的半径为R m,则OD- （R-0.25）m
AD= 1/2AB=1/2×0.72=0. 36（m）
在Rt △OAD中,OA2=OD2 +AD2
∴ R2=（R-0.25）2+0.362
解得R≈0.384
∴这个车轮的半径约是0.384m
第三章复习题第4题答案
解：CD=CE，理由如下：如下图所示：
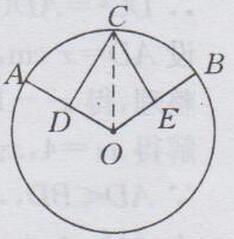
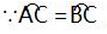
连接OC
∴∠AOC=∠BOC
又∵OA=OB，OD=DA，OE=EB
∴OD=OE
又∵OC=OC
∴△ODC≌△OEC
∴CD=CE
第三章复习题第5题答案
解：OD//AC，理由如下：
∵∠CDD=60°，
∴∠CAD=1/2∠COD=30°
又∵AO=OD
∴∠ODA=∠BAD=30°
∴∠CAD=∠ODA
∴OD//AC
第三章复习题第6题答案
（1）∠AEB=∠ADB=∠ACB
（2）∠BAC=∠BEC=∠BDC
（3）∠CAD=∠CBD=∠CED
（4）∠DAE=∠DBE=∠DCE（注：此题答案不唯一）
第三章复习题第7题答案
解：如下图所示：
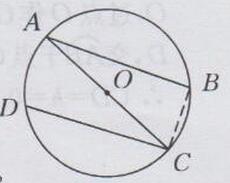
连接BC
∵AC为⊙O的直径
∴∠ABC= 90°
∴∠A+∠BCA=90°
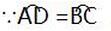
∴∠DCA=∠A.
∴∠DCA+∠ACB=90°，即∠DCB=90°
第三章复习题第8题答案
解：∵AB是⊙O的直径
∴∠ACB=90°
∵CD⊥AB,
∴△ACD≌ △CBD
∴DC/DB=AD/CD
即DC2=AD·BD
∴DC2=AD（AB-AD）
设AD=x cm，则62= x（13-x）
整理，得x2-13x+36=0
解得x1=4，x2=9
∵AD<BD
∴只能取x=4
∴AD=4cm
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
教科版物理书九年级下册答案
九年级下册语文作业本答案人教版
北师大版九年级上册数学书答案
九年级上册物理同步练习答案苏科版
九年级下册语文新课程自主学习与测评答案人教版
九年级下册数学补充习题答案苏科版
九年级上册语文同步解析与测评答案人教版
苏人版九年级上册思想品德伴你学答案
九年级下册数学书答案华东师大版
九年级下册英语课课练答案译林版