习题3.9第1题答案
解：∵PA与PB分别切⊙O于A，B两点，DE切⊙O于点C
∴DA=DC，CE=EB
∵△PDE的周长=PD+DE+EP
=PD+DC+CE+EP
=PD+DA+EB+EP
=PA+PB，
又∵PA=PB=5cm
∴△PDE的周长=2×5=10（cm）
习题3.9第2题答案
解：由切线长定理知AE=AF，BF=BD，CE=CD
令AE=AF=xcm,BF =BD=ycm,CE=CD=z cm
∵AC=AE+CE=x+z=13
AB=AF+BF=x+ y=9，BC=BD+CD=y+z=14
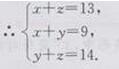
∴AF=4cm，BD=5cm，CE=9cm
习题3.9第3题答案
解：如下图所示：
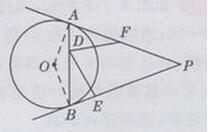
连接OA，OB
∵PA，PB切⊙O于点A，B
∴OA⊥PA，OB⊥PB
∴∠OAP=∠ OBP=90°
在四边形OAPB中，∠AOB+∠P=180°
又∵∠P= 40°
∴∠AOB=140°
∵OA =OB
∴∠OAB=∠OBA=20°
又∵OA⊥PA，OB⊥PB
∴∠FAD=∠EBD=90°-20°=70°
又∵在△DBE和△FAD中
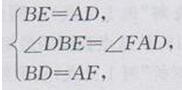
∴△DBE≌△FAD（SAS）
∴∠ADF=∠BED,∠BDE=∠AFD.
∴∠ADF+∠BDE=∠ADF+∠AFD=180°-∠FAD=180°- 70°=110°
又∵∠ADF+∠BDE+∠EDF=180°
∴∠EDF=180°一（∠ADF+∠BDE） =180°-110°=70°
习题3.9第4题答案
（1）能，首先以B点为端点将BA与BC重合在一起折出∠ABC的平分线所在的线段，其次将BC与DC重合折出∠BCD的平分线所在的线段，两条线段的交点即为圆心O，量出圆心到BC边的距离约为3.4 cm
（2）如下图所示：
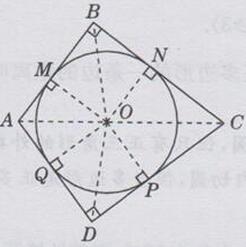
连接AC,根据折叠得到圆心O在线段AC上，设⊙O与四边形ABCD四边AB，BC，CD，DA均相切，且切点分别为M，N，P，Q.
在△ABC和△ADC中
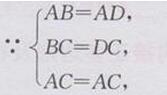
∴△ABC≌△ADC(SSS)
∴∠D=∠B=90°
∴S△ABC=S△ADC
连接OM，ON，OQ，OP，设⊙O的半径为r，连接OB，OD
∴S四边形ABCD=2△ABC =2×1/2 AB·BC= AB .BC=6×8=48(cm2)
又∵S四边形ABCD =1/2 AB·r+1/2 BC．R+1/2 AD·r+1/2 CD·r
=1/2×6×r+1/2×8×r+1/2×6×r +1/2×8×r
=3r+4r+3r+4r=14r
∴14r=48
∴r=24/7（cm）
∴最大圆形纸片的半径为24/7cm
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
人教版九年级上册数学课时练答案
九年级下册化学书答案上教版
九年级下册数学配套练习册答案青岛版
数学九年级下册学习与评价答案苏科版
九年级下册数学书答案沪科版
九年级下册历史新编基础训练答案北师大版
九年级下册数学课时特训答案浙教版
九年级上册语文课课练答案苏教版
九年级下册语文课课练答案苏教版
上教版九年级下册英语知识与能力训练答案