答案网 - 课本习题,辅导练习，辅导材料等答案解析！
语文 数学 英语
书通网logo
当前位置: 书通网 > 答案 > 九年级下册书答案 > 北师大版九年级下册数学书答案 >

北师大版九年级下册数学书习题3.3答案

时间:2016-12-08 来源:书通网 共计4题

习题3.3第1题答案

解：如下图所示：

1.jpg

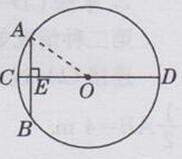
连接OA，设⊙O的半径为r寸，则OE=（r-1）寸

∵CD为直径，且CD⊥AB

∴AE=BE=1/2AB=5寸

在Rt△AOE中

∵OA2=AE2+OE2

∴r2=52+（r-1）2

解得r=13

∴CD=26寸

∴直径CD的长为26寸

习题3.3第2题答案

解：如下图所示：

2.jpg

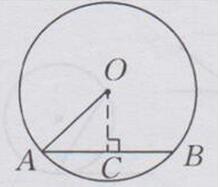
过点O作OC⊥AB于点C

则AC=1/2AB=1/2×36=18（mm）

在Rt△ACO 中

2.1.jpg

2.2.jpg

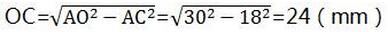
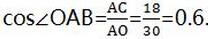
故点O到AB的距离为24mm，∠OAB的余弦值为0.6 

习题3.3第3题答案

解：如下图所示：

3.jpg

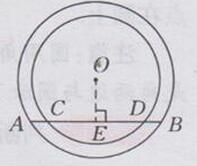
AC=BD，理由如下：

过点 O作OE⊥AB于点E

∵在大⊙O中，AE=EB，在小⊙O中，CE=ED

∴AE-EC=EB-ED，即AC=BD

习题3.3第4题答案

解：如下图所示：

4.jpg

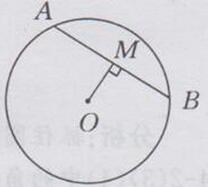
作法：

（1）连接OM

（2）过点M作OM的垂线，交⊙O于点A，B.线段AB即为所求的弦

北师大版九年级下册数学书答案

更多

推荐阅读

点击查看更多内容
优美的诗句 伤感的句子 好词好句 唯美的句子 思念的诗句 经典语句

声明 :本网站尊重并保护知识产权，根据《信息网络传播权保护条例》，如果我们转载的作品侵犯了您的权利,请在一个月内通知我们，我们会及时删除。

皖ICP备11009057号