第二章复习题第23题答案
解：如下图所示：
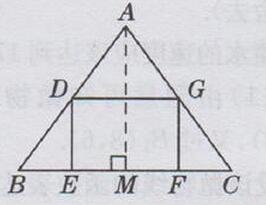
过点A作AM⊥BC，交BC于点M
∵AB=AC
∴BM=MC=1/2BC=1/2×12=6
在Rt△AMB中，∠AMB=90°
又∵AB=10，由勾股定理，得AM2+BM2=AB2
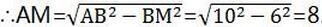
∵DG//BC
∴△ADG∽△ABC
∵DG=EF
∴AD/AB=DG/BC=x/12
∴BD/AB=(AB-AD)/AB=1-AD/AB=1-x/12=(12-x)/12.
又∵DE//AM
∴△BDE∽△BAM
∴DE/AM=BD/AB=(12-x)/12
∴DE=AM·BD/AB=8×(12-x)/12=(2(12-x）)/3
∴S矩形DEFG=EF·DE=x·(2(12-x）)/3=-2/3x2+8x，即y=-2/3x2+8x
∴y与x之间的函数表达式为y=-2/3x2+8x.
∴y=-2/3（x2-12x）=-2/3（x2-12x+62-62）=-2/3（x-6）2+24
列表，得：
| x | 0 | 3 | 6 | 9 | 12 |
| y | 0 | 18 | 24 | 18 | 0 |
画出函数图像，如下图所示：
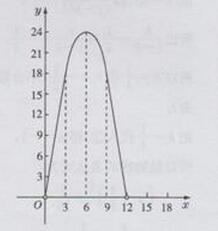
∴（1）自变量x的取值范围是0<x<12
（2）二次函数图像的对称轴是直线x=6，，顶点坐标是（6,24）
（3）当0<x<6时，y的值随着x值的增大而增大；当x=6时，y的值最大；当6<x<12时，y的值岁x值的增大而减小
第二章复习题第24题答案
解：设销售单价y与月份x的函数表达式为y=kx+b（k≠0）
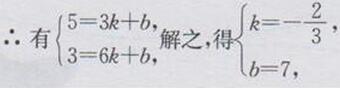
∴y=-2/3x+7（x=3,4,5,6）
设蔬菜成本m与x的函数表达式是
m=a（x-h）2+n（a≠0），
由题意，得h=6，n=1，
∴4=a（3-6）2+1
∴a=1/3
∴m=1/3（3-6）2+1=1/3x2-4x+13（x=3,4,5,6）
∴每千克的收益w=y-m=-2/3x+7-（1/3x2-4x+13）
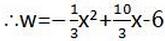
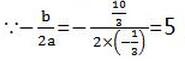
因而，在5月份出售这种蔬菜每千克的收益最大
第二章复习题第25题答案
（1）∵当n=1时，有1个小正方形，此时1=12；
当n=2时，有4个小正方形，此时4=22；
当n=3时，有9个小正方形，此时9=32；
…
∴第n个图形，有n2个小正方形.
（2）依次为4,9,16,25，…，n2.
第二章复习题第26题答案
解：（1）从第1个到第5个图形中圆圈的个数分别为1,1+2=3,1+2+3=6,1+2+3+4=10,1+2+3+4+5=15
因而第6个图形中圆圈的个数是1+2+3+4+5+6=21个
（2）填表：
| 边上的小圆圈数 | 1 | 2 | 3 | 4 | 5 |
| 每个图中小圆圈的总数 | 1 | 3 | 6 | 10 | 15 |
（3）m=1/2n（n+1）=1/2n2+1/2 n
第二章复习题第27题答案
（1）四个图中小圆圈的个数分别是1,7,19,37，第5个图中有61个小圆圈
（2）填表：
| 边上小圆圈数 | 1 | 2 | 3 | 4 | 5 |
| 每个图中小圆圈的总数 | 1 | 7 | 19 | 37 | 61 |
（3）m=6×1/2n（n-1）+1=3n2-3n+1
第二章复习题第28题答案
121个
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册科学作业本答案浙教版
九年级下册物理同步练习答案苏科版
九年级下册数学新编基础训练答案北师大版
九年级下册数学书答案人教版
九年级下册历史新编基础训练答案人教版
数学九年级上册学习与评价答案苏科版
九年级下册历史与社会思想品德课时特训答案人教版
九年级上册语文同步训练答案人教版
人教版九年级上册化学书答案