第二章复习题第17题答案
（1）建立直角坐标系如下图所示：
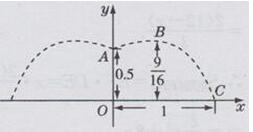
（2）设右边抛物线的表达式为y=a（x-h）2+9/16（a≠0）
因为图像过A（0，0.5），B（h，9/16），C（1，0）三点
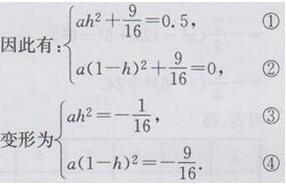
因为a≠0，h≠0
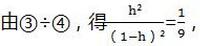
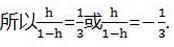
所以h=1/4或h=-1/2（不合题意，舍去）
把h=1/4代入③，得a=-1
所以，抛物线的表达式为：
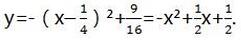
自变量的取值范围是0≤x≤1
第二章复习题第18题答案
解：设其中一个数为x，则另一个数为a-x，设其乘积为y，根据题意得：
y=x（a-x）=-x2+ax.当x=-a/(2×（-1）)=a/2时，y有最大值
因此把一个数分解成两个数之和，当这两个数相等时，它们的乘积最大
第二章复习题第19题答案
（1）根据题意得：
y=（26-2x）∙（22-2x）=4x2-96x+572.
（2）图像略
（3）当x=1时，可放入（26-2）×（22-2），即24cm×20cm的相片
当x=1.5时，可放入23cm×19cm的相片
当x=2时，可放入22cm×18cm的相片
第二章复习题第20题答案
解：由题意知，该抛物线的最高点的纵坐标为：
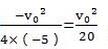
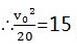
∴v0=17.32或v0=-17.32（不合题意，舍去）
答：喷水的速度应该达到了17.32m/s
第二章复习题第21题答案
（1）由题意可知：
抛物线的顶点是（0，8），有过点B1（8,6）
∴该抛物线的函数表达式为y=ax2+8（a≠0）
∴6=a×82+8
∴a=-1/32
∴该抛物线的函数表达式为y=-1/32x2+8（-8≤x≤8）
（2）由于设两个车道，汽车只能走一个车道，
∴将x=±4代入函数表达式，得y=71/2>7
因此，这辆货车能通过这个隧道
第二章复习题第22题答案
解：如下图所示：
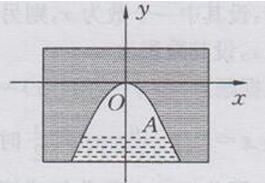
以抛物线的顶点为原点建立平面直角坐标系
设该抛物线的表达式为y=ax2（a≠0）
由题意知，抛物线过点（2,-2），
∴-2=a×22
∴a=-1/2
∴抛物线的表达式为y=-1/2x2
当水面下降1m时，拱高为2+1=3（m）
∴-3=-1/2x2，
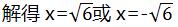
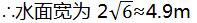
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册科学作业本答案浙教版
九年级下册物理同步练习答案苏科版
九年级下册数学新编基础训练答案北师大版
九年级下册数学书答案人教版
九年级下册历史新编基础训练答案人教版
数学九年级上册学习与评价答案苏科版
九年级下册历史与社会思想品德课时特训答案人教版
九年级上册语文同步训练答案人教版
人教版九年级上册化学书答案