第六章复习题第13题答案
解：过n边形某个顶点的对角线，将这个多边形分成（n-2）个三角形
根据题意，得n-2=7
解得n=9
所以这个多边形是九边形
第六章复习题第14题答案
是正四边形
第六章复习题第15题答案
证明：如下图所示：
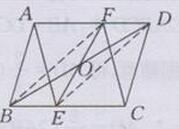
连接BF,DE在□ABCD中，AD∥BC，AD=BC
∴AF∥EC
又∵AE∥FC
∴四边形AECF是平行四边形
∴AF=EC
∴AD-AF=BC-EC,即FD=BE
∵FD∥BE
∴四边形FDEB为平行四边形（一组对边平行且相等的四边形是平行四边形）
∵平行四边形对角线互相平分
∴EF过BD的中点O
第六章复习题第16题答案
证明：∵EDAC,BF⊥AC
∴∠AED=∠CFB=90°
∵∠ADB=∠CBD
∴AD∥BC
∴∠DAE=∠BCF（两直线平行，内错角相等）
在△ADE和△CBF中
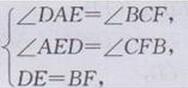
∴△ADE≌△CBF（AAS）
∴AD=CB
∵AD∥BC
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）
第六章复习题第17题答案
（1）DE,BF,FC之间的位置关系：DE∥BF,DE∥FC,BF 与FC在同一条直线BC上
（2）DE,BF,FC之间的数量关系：DE=BF=FC
证明如下：
（1）∵AD=DB
∴D是AB的中点
∵AE=EC
∴E是AC的中点
∴DE是△ABC的中位线
∴DE∥BC,即DE∥BF,DE∥FC,BF与FC在同一条直线BC上
（2）∵FG∥AB,AG∥BC
∴AG=BF
又∵AG∥BC
∴∠GAE=∠C
在△AEG和△CEF中
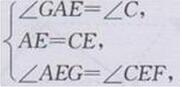
∴△AEG≌△CEF（ASA）
∴AG=CF
∴BF=CF=1/2BC.DE是△ABC的中位线
∴DE=1/2BC,∴DE=BF=FC
第六章复习题第18题答案
解：有6个平行四边形
这6个平行四边形分别是：□ FABO, □ ABCO, □BCDO, □ CDEO, □ DEFO, □ EFAO
选择 □ FABO加以证明
证明如下：
∵△AOF和△AOB都是等边三角形
∴AF=OA,OA=OB
∴AF=OB
∵∠FAO=60°, ∠AOB=60°
∴∠FAO=∠AOB
∴AF∥BO（内错角相等，两直线平行）
∵AF=BO
∴四边形FBAO是平行四边形（一组对角相等且平行的四边形是平行四边形）
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册英语长江全能学案阅读训练答案人教版
河北少儿版八年级下册生物作业本答案江西省
八年级下册数学新编基础训练答案北师大版
人教版八年级上册生物知识与能力训练答案
人教版八年级上册物理知识与能力训练答案
八年级下册英语同步解析与测评答案人教版
八年级下册历史新编基础训练答案北师大版
青岛版八年级上册数学书答案