习题6.6第1题答案
证明：∵D,E,F分别 是边BC,CA,AB的中点
∴DE,DF是△ABC的中位线
∴DE∥AB,DF∥AC，且AB=2DE,AC=2DF
∴四边形AFDE是平行四边形
∴四边形AFDE的周长=2DE+2DF=AB+AC
习题6.6第2题答案
已知：在△ABC中，EF是△ABC的中位线，AD是BC边上的中线，求证：EF与AD互相平分，
证明：如下图所示：
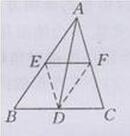
连接DE,DF
∵AD是BC边上的中点
∴点D是BC的中点
∵EF是△ABC的中位线
∴DE,DF也是△ABC的中位线
∴DE∥AC,DF∥AB,即DE∥AF,DF∥AE
∴四边形DEAF是平行四边形（两组对边分别平行的四边形是平行四边形）
∴EF与AD互相平分
习题6.6第3题答案
解：四边形EGFH是平行四边形
∵E,G分别是ABAC的中点
∴EG是△ABC的中位线，EG∥BC,且EG=1/2BC
∵H,F分别是DB,DC的中点
∴H,F分别是DB,DC的中点
∴HF是△ABC的中位线
∴HF∥BC,且HF=1/2BC
∴EG∥HF,EG=HF
∴四边形EGFH是平行四边形（一组对边平行且相等的四边形是平行四边形）
习题6.6第4题答案
解：如果M,N两点之间还有阻隔，可以步测出CM的中点E,CN的中点F，并测出EF的长就可以知道MN的长，今儿知道A,B间的距离
理由：如下图所示：
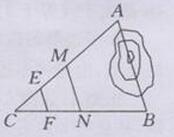
∵E是CM的中点
∴EF是△CMN的中位线
∴AB=2MN=2×2EF=4EF
∴测出EF的长就可以知道了A,B间的距离
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册语文作业本答案人教版
八年级下册思想品德课时练答案人教版
八年级下册数学书答案青岛版
八年级下册数学课时练答案人教版
八年级下册地理同步解析与测评答案人教版
八年级下册物理同步解析与测评答案人教版
八年级上册生物学法大视野答案苏教版
八年级下册数学课时作业本答案人教版
人教版八年级上册语文课时特训答案
物理八年级下册学习与评价答案苏科版