第十二章复习题第7题答案
证明:∵∠A=∠F(已知)
∴DF∥AC(内错角相等,两直线平行)
∴∠D=∠ABM(两直线平行,内错角相等)
∵∠1=∠DMN(对顶角相等).∠1=∠2(已知)
∴∠DMN=∠2(等量代换)
∴DB∥EC(同位角相等,两直线平行)
∴∠C=∠ABM(直线平行,同位角相等)
∴∠C=∠D(等量代换)
第十二章复习题第8题答案
证明:∵五边形GBCDH的内角和为(5-2)×180°=540°(多边形的内角和公式)
即∠HGB+∠ABC+∠C+∠CDE+∠GHD=540°,∠ABC+∠C+∠CDE=360°(已知)
∴∠HGB+∠GHD=180°(等式性质)
∴AB∥ED同旁内角互补,两直线平行)
∴∠1=∠GHD(两直线平行,同位角相等)
∵∠2=∠GHD(对顶角相等)
∴∠1=∠2(等量代换)
第十二章复习题第9题答案
和等于180°
证明如下:
如下图所示:

由∠BFG=∠E+∠C,∠BFG=∠A+ ∠D,∠B+∠BFG+∠BGF=180°
得∠A+∠B+∠C+∠D+∠E=180°
第十二章复习题第10题答案
证明:∵∠ACB=90°(已知)
∴∠BAC+∠B=90°(直角三角形的两锐角互余)
同理∠BAC+∠ACD=90°
∴∠B=∠ACD(等量代换)
∵AE是角平分线(已知)
∴∠BAE=∠CAE(角平分线的定义)
∴∠B+∠BAE=∠ACD+∠CAE(等式性质)
∵∠CEF=∠B+∠BAE,∠CFE=∠ACD+∠CAE(三角形的一个外角等于和它不相邻的两个内角的和)
∴∠CFE=∠CEF(等量代换)
第十二章复习题第11题答案
证明:设两个连续的奇数为2n-1,2n+1(n>0且月为整数)
则(2n+1)2 -(2n -1)2=(2n+1+2n-1)•(2n+1-2n+1)=2•4n=8n
即两个连续奇数的平方差一定为8的倍数(或一定为偶数)
第十二章复习题第12题答案
解:(1)如下图所示:
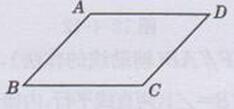
①如果AB∥CD,∠B =∠D,那么:AD∥BC
②如果AD∥BC,∠B=∠D,那么:AB∥CD
③如果AB∥CD,AD∥BC,那么:∠B=∠D
(2)是真命题,证明如下:
①∵AB∥CD(已知)
∴∠B+∠C=180°(两直线平行,同旁内角互补)
又∵∠B=∠D(已知)
∴∠D+∠C=180°(等量代换)
∴AD// BC(同旁内角互补,两直线平行)
②∵AD∥BC
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∵∠B=∠D(已知)
∴∠A+∠D=180°(等量代换)
∴AB∥CD(同旁内角互补,两直线平行)
③∵AB∥CD(已知)
∴∠A+∠D=180°(两直线平行,同旁内角互补)
∵AD∥BC(已知)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D(同角的补角相等)

 苏科版七年级下册数学书答案
苏科版七年级下册数学书答案 北师大版七年级下册数学书答案
北师大版七年级下册数学书答案 语文版七年级下册语文课本答案
语文版七年级下册语文课本答案 浙教版七年级下册科学课本答案
浙教版七年级下册科学课本答案 浙教版七年级下册数学课本答案
浙教版七年级下册数学课本答案 北师大版七年级下册生物课本答案
北师大版七年级下册生物课本答案 北师大版七年级下册历史课本答案
北师大版七年级下册历史课本答案 北师大版七年级下册语文课本答案
北师大版七年级下册语文课本答案 苏教版七年级下册语文课本答案
苏教版七年级下册语文课本答案 七年级下册数学书答案人教版
七年级下册数学书答案人教版 七年级下册地理课时练答案人教版
七年级下册地理课时练答案人教版 七年级下册历史南方新课堂答案人教版
七年级下册历史南方新课堂答案人教版 七年级下册英语同步精练答案外研版
七年级下册英语同步精练答案外研版 人教版七年级上册数学作业本答案江西省
人教版七年级上册数学作业本答案江西省 人教版七年级上册语文作业本答案江西省
人教版七年级上册语文作业本答案江西省 七年级下册历史新编基础训练答案华师大版
七年级下册历史新编基础训练答案华师大版 人教版七年级上册语文书答案
人教版七年级上册语文书答案 七年级下册数学同步训练答案人教版
七年级下册数学同步训练答案人教版 七年级上册历史学法大视野答案人教版
七年级上册历史学法大视野答案人教版