习题12.2第1题答案
（1）2,3,4,32-2×4 =9 -8 =1
（2）3,4,5,42-3×5=16 -15 =1，发现这个差为1
（3）结果为1．可设中间一个数为n，则两边的数为n-1，n+1，则n2-(n-1)，(n+1)=n2-(n2-1)=1
习题12.2第2题答案
不是
解：设甲地到乙地全程是s km，骑自行车的速度是15 km/h，往返全程用的时间是(s/5+s/15)h，则往返全程的平均速度是：
不是步行速度的2倍
习题12.2第3题答案
(1)2；E
(2)1；B
(3)AC；ED
(4)CE；AB
(5)2；A；内错角相等,两直线平行
(6)D；ACD
习题12.2第4题答案
已知；2；ECD；角平分线的定义；ECD；等量代换；内错角相等，两直线平行
习题12.2第5题答案
证明：∵AB∥CD（已知）
∴∠B=∠C（两直线平行，内错角相等）
∵BC∥DE（已知）
∴∠C+∠CDE=180°（两直线平行，同旁内角互补）
∴∠B+∠CDE=180°（等量代换）
习题12.2第6题答案
证明：∵AD平分∠BAC（已知）
∴∠BAD=∠CAD（角平分线的定义）
∵AD∥EF(已知)，∠BAD=∠AGF(两直线平行，内错角相等)，∠CAF=∠F(两直线平行，同位角相等)
∴∠AGF=∠F(等量代换)
习题12.2第7题答案
已知：如下图所示，直线AB、CD被直线EF所截，AB∥CD，MG平分∠BMN，NG平分/MND
求证：MG⊥NG
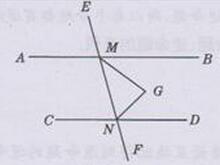
证明：∵AB∥CD(已知)
∴∠BMN+∠MND=180°(两直线平行，同旁内角互补）
∵MG平分∠BMN，NG平分∠MND（已知）
∴2∠NMG=∠BMN，2∠MNG=∠MND(角平分线的定义)
∴2∠NMG+2∠MNG=180°（等量代换），∠NMG+∠MNG=90°
又∵∠NMG+∠G+∠MNG=180°（三角形内角和定理)
∴∠G=90°
∴MG⊥NG（垂直定义）
习题12.2第8题答案
证明：∵∠FEC=∠A+∠ADE，∠ABC=∠F+∠FDB(三角形的一个外角等于和它不相邻的两个内角的和)，∠A=∠ABC (已知)
∴A=∠F十∠FDB(等量代换)
∵∠FDB=∠ADE(对顶角相等)
∴∠A=∠F+∠ADE(等量代换)
∴∠ADE=∠A-∠F（等式性质）
∴∠FEC=∠A+∠A-∠F(等量代换)
∴∠F+∠FEC=2∠A(等式性质)
苏科版七年级下册数学书答案
北师大版七年级下册数学书答案
语文版七年级下册语文课本答案
浙教版七年级下册科学课本答案
浙教版七年级下册数学课本答案
北师大版七年级下册生物课本答案
北师大版七年级下册历史课本答案
北师大版七年级下册语文课本答案
苏教版七年级下册语文课本答案
七年级下册数学书答案人教版
英语七年级下册学习与评价答案译林版
七年级下册地理新课程自主学习与测评答案人教版
七年级上册数学学法大视野答案人教版
苏教版七年级上册语文补充习题答案
语文七年级下册学习与评价答案苏教版
七年级下册历史同步解析与测评答案人教版
七年级下册地理同步精练答案粤人民版
七年级上册生物课课练答案苏科版
七年级下册数学作业本答案浙教版
七年级下册语文同步解析与测评答案人教版