习题5.5第1题答案
已知：△ABC，如下图所示：
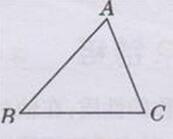
求作△ABC的三个内角的平分线.
作法如下：
（1）在BA和BC上分别截取BD,BE，使BD=BE.
（2）分别以D,E为圆心，以大于1/2DE的长为半径作弧，两弧在∠ABC内交于点O.
（3）作射线BO交AC于点M.同理可以作出∠BAC, ∠ACB的平分线AN，CP分别交BC，AB于点N,P，线段AN，BM,CP就是△ABC的三个内角的平分线，如下图所示：
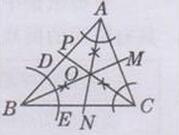
习题5.5第2题答案
过点M作MN⊥AB于点N，如下图所示：
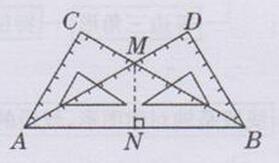
因为∠CAB=60°，∠BAM=30°
所以∠CAM=∠BAC-∠BAM=60°-30°=30°
所以AM平分∠CAB
因为∠C=90°
所以CM=MN（角平分线上的点到这个角的两边 的距离相等）
习题5.5第3题答案
如下图所示：
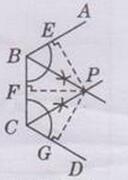
过点P作PE⊥AB,PF⊥BC,PG⊥CD,分别交BA，BC,CD于点E,F,G
因为BP平分∠ABC
所以PE=PF
因为CP平分∠BCD
所以PF=PG
所以PE=PF=PG
所以根据角平分线的性质，可得点P到三面墙的距离都相等
推荐阅读
苏科版七年级下册数学书答案
年级：七年级
版本：苏科版
科目：数学
学期：下册
名称：课本
北师大版七年级下册数学书答案
年级：七年级
版本：北师大版
科目：数学
学期：下册
名称：课本
语文版七年级下册语文课本答案
年级：七年级
版本：语文s版
科目：语文
学期：下册
名称：课本
浙教版七年级下册科学课本答案
年级：七年级
版本：浙教版
科目：科学
学期：下册
名称：课本
浙教版七年级下册数学课本答案
年级：七年级
版本：浙教版
科目：数学
学期：下册
名称：课本
北师大版七年级下册生物课本答案
年级：七年级
版本：北师大版
科目：生物
学期：下册
名称：课本
北师大版七年级下册历史课本答案
年级：七年级
版本：北师大版
科目：历史
学期：下册
名称：课本
北师大版七年级下册语文课本答案
年级：七年级
版本：北师大版
科目：语文
学期：下册
名称：课本
苏教版七年级下册语文课本答案
年级：七年级
版本：苏教版
科目：语文
学期：下册
名称：课本
七年级下册数学书答案人教版
年级：七年级
版本：人教版
科目：数学
学期：下册
名称：课本
七年级上册语文配套练习册答案人教版
年级：七年级
版本：人教版
科目：语文
学期：上册
名称：配套练习册
浙教版七年级上册数学课时特训答案
年级：七年级
版本：浙教版
科目：数学
学期：上册
名称：课时特训
人教版七年级上册地理长江作业本答案
年级：七年级
版本：人教版
科目：地理
学期：上册
名称：长江作业本
北师大版七年级上册数学作业本答案江西省
年级：七年级
版本：北师大版
科目：数学
学期：上册
名称：作业本
人教版七年级上册语文新课程自主学习与测评答案
年级：七年级
版本：人教版
科目：语文
学期：上册
名称：新课程自主学习与测评
七年级下册语文课时作业本答案人教版
年级：七年级
版本：人教版
科目：语文
学期：下册
名称：课时作业本
语文七年级下册学习与评价答案苏教版
年级：七年级
版本：苏教版
科目：语文
学期：下册
名称：学习与评价
七年级下册语文南方新课堂答案人教版
年级：七年级
版本：人教版
科目：语文
学期：下册
名称：南方新课堂
苏教版七年级上册思想品德补充习题答案
年级：七年级
版本：苏教版
科目：思想品德
学期：上册
名称：补充习题
七年级下册生物南方新课堂答案人教版
年级：七年级
版本：人教版
科目：生物
学期：下册
名称：南方新课堂