第20页作业题第1题答案
已知垂直的定义三角形的外角等于与它不相邻的两个内角的和
第20页作业题第2题答案
证明：∵∠BDC是△ABD的外角，
∴∠BDC=∠ABD+∠A（三角形的外角等于与它不相邻的两个内角的和）
又∵∠BDC=75°，∠A=40°（已知）
∴∠ABD=75°-40°=35°
又∵BD是∠ABC的平分线（已知）
∴∠ABC=2∠ABD=70°（角平分线的定义）
∵∠C= 180°-∠A-∠ABC=180°-40°-70°=70°
（三角形内角和定理）
∴∠ABC=∠C（等量代换）
第20页作业题第3题答案
解：∵∠3是△ABC的外角
∴∠3= ∠1+∠2（三角形的外角等于与它不相邻的两个内角的和）
又∵∠3=100°，∠1=∠2
∴∠1=50°
第20页作业题第4题答案
已知：如下图所示：
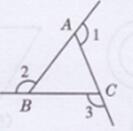
∠1，∠2，∠3是△ABC不共顶点的三个外角
求证：∠1+∠2+∠3=360°
证明：∵∠1 +∠BAC= 180°（平角的定义）
∠2+∠ABC= 180°（平角的定义）
∠3+∠ACB=180°（平角的定义）
∴∠1+∠BAC+∠2+∠ABC+23+∠ACB=540°
又∵∠BAC+ ∠ABC+ ∠ACB=180°（三角形内角和定理）
∴∠1+∠2+∠3=540°-180°=360°（等式的性质）
第20页作业题第5题答案
证明：如下图所示：
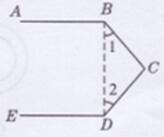
连结BD，则∠1+∠2+∠C=180°（三角形内角和定理）
又∵∠ABC+ ∠C+∠CDE=360°（已知）
∴∠ABD+∠BDE= 360°-180°=180°（等式的性质）
∴AB//DE（同旁内角互补，两直线平行）
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
浙教版八年级下册科学课本答案
八年级下册思想品德新课程自主学习与测评答案人教版
北师大版八年级下册历史课本答案
八年级下册科学作业本答案浙教版
八年级下册语文书答案人教版
人教版八年级上册语文作业本答案
八年级下册思想品德课时练答案人教版
八年级下册物理阳光学业评价答案人教版
八年级下册生物长江作业本答案人教版
人教版八年级上册英语长江作业本答案