复习题第1题答案
明：如下图所示：
作直线d分别交a，b，c于点E，F，G
∵a//c，b//c（已知）
∴∠1=∠3，∠12=∠3（两直线平行，同位角相等）
∴∠1=∠2（等式性质）
∴a//b（同位角相等，两直线平行）
复习题第2题答案
证明：如下图所示：
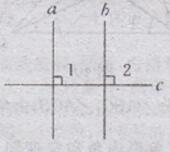
∵a⊥c，b⊥c(已知)
∴∠1= 90°，∠2=90°（垂直的性质）
∴∠1=∠2（等式性质）
∴a//b（同位角相等，两直线平行）
复习题第3题答案
解：(1)∠A十∠C=∠E，如下图所示：
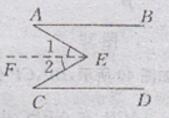
证明：作EF//AB
∴∠A=∠1（两直线平行，内错角相等）
又∵AB//CD(已知)
∴EF//CD(平行于同一直线的两直线平行)
∴∠2 =∠C（两直线平行，内错角相等）
∴∠AEC=∠1十∠2=∠A+∠C（等式性质）
(2)∠A十∠E+∠C= 360°.（证明略）
(3)∠A-∠C=∠E，如下图所示：
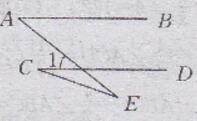
证明：∵AB//CD(已知)
∴∠A= ∠1(两直线平行，内错角相等)
又∵∠1=∠C+∠E（三角形的一个外角等于和它不相邻的两个内角之和）
∴∠A-∠C=∠E
复习题第4题答案
(1)如下图所示：
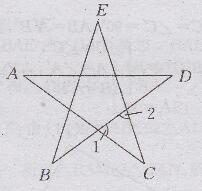
∵∠1=∠A+∠D，∠2=∠B+∠E（三角形的一个外角等于与它不相邻的两个内角的和）
又∵∠1十∠2+∠C=180°（三角形内角和定理）
∴∠A+∠D+∠B十∠E+∠C=180°，即∠A+∠B+∠C+∠D+∠E=180°
(2)如下图所示：
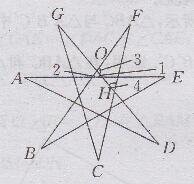
根据三角形外角性质得∠1=∠A+∠D，∠2=∠B+∠E，∠4=∠G+∠C，∠3=∠1+∠2
∵在△FOH中，∠3+∠4+∠F=180°
∴∠A+∠D+∠B+∠E十∠G+∠C十∠F=180°，即∠A+∠ B+∠C+∠D+∠E+∠F +∠G=180°
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
八年级上册物理配套练习册答案沪科版
八年级下册地理同步导学与优化训练答案人教版
八年级下册物理课时作业本答案人教版
教科版八年级下册物理作业本答案江西省
八年级下册物理课课练答案苏科版
人教版八年级下册英语课本答案
物理八年级下册学习与评价答案苏科版
八年级上册语文配套练习册答案人教版
苏科版八年级上册数学补充习题答案
人教版八年级上册历史知识与能力训练答案