复习题第13题答案
证明：连接BE
∵E是△ABC的内心
∴∠ABE=∠EBC, ∠BAE=∠DAC, ∠EBD=∠EBC+∠CBD, ∠BED=∠ABE+∠BAE
又∵∠CBD=∠DAC
∴∠CBD=∠BAE
∴∠DBE=∠BED
∴DE=DB
复习题第14题答案
解：这个锚标浮筒的表面积为：
S=S圆柱侧面+2S圆锥侧面
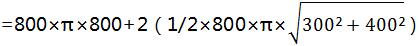
=64000π+40000π=1040000π（mm2）
则电镀这样的锚标浮筒100个
共需锌0.11×（1040000π÷106×100）=0.11×104π =11.44π（kg）
答：需用锌11.44πkg
复习题第15题答案
解：过点D作DF⊥BC于F
由切线性质可知DE=DA=x,CE=CB=y
∵AB⊥ AD, AB⊥BC,DF⊥BC
∴四边形ABFD是矩形
∴DF=AB=12，FC=y-x
又DC=y+x
在Rt△DCF中，DF2+FC2=DC2
∴122+(y-x)2=(y+x)2
∴y=36/x
由△DFC的三边关系可知（y+x）-（y-x）<12<（y+x）+（y-x）
∴x<6,从而可知x的取值范围是0<x<6
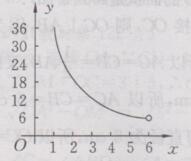
∴y与x的函数关系式是y=36/x(0<x<6),其图像如下图所示：
复习题第16题答案
证明：连接AD,则AD⊥BC，易证O在AD上，连接DF
因为G,F,D分别为AB,AC, BC的中点
所以GF∥＝BD
所以四边形BGFD为平行四边形，∠B+∠BGF=180°
因为∠A=36〬，AB=AC
所以∠B=1/2(180°-∠A)=1/2×(180°-36°)=72°
所以∠BGF=180°-∠B=180°-72°=108°
同理可证：∠GFE =108°
因此易得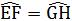
所以EF=HG
因为AD为O的直径所在的直线
所以AD等分O，AD⊥GF
所以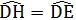
所以DH=DE
因为四边形GHDF为O的内接四边形
所以∠HGF+∠HDF=180〬
所以∠HDF=180°-∠HGF=180°-108°=72°
因为四边形BDFG 为平行四边形
所以BD//DF
所以∠GHD+∠HDF=180°
所以∠GHD=180°-∠HDF =180°-72°=108°
同理可得∠FDE=108°
所以∠HDE=540°-108°×4=108°
因为∠BHD+∠GHD=180°
所以∠BHD=180°-108°=72°
因为∠B=72°
所以∠B=∠BHD
所以BD=DH
所以DH=GF=DE
因为FD=FC,∠C=72°
所以∠DFC=180°-72°×2=36°
因为∠DEF=108°
所以∠EDF=180°-∠DEF-∠DFC=180°-108°-36°=36°
所以∠DEF=∠DFC
所以EF=ED
所以EF=DE=DH=GH=GF
所以五边形DEFGH是正五边形
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级下册物理同步解析与测评答案人教版
教科版九年级下册物理作业本答案江西省
语文九年级上册学习与评价答案苏教版
九年级下册历史同步解析与测评答案人教版
人教版九年级上册数学作业本答案江西省
人教版九年级上册化学新课程自主学习与测评答案
九年级上册语文学法大视野答案人教版
人教版九年级上册语文知识与能力训练答案
语文版九年级下册语文课本答案
沪粤版物理书九年级下册答案