人教版九年级上册数学书第24章复习题答案

复习题第1题答案

（1）	（2）	（3）	（4）	（5）
B	D	B	C	B

复习题第2题答案

证明：连接OC

因为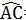和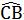

所以∠AOC=∠COB

因为D、E分别是半径OA,OB的中点

所以OD=1/2OA,OE=1/2OB

又因为OA=OB

所以OD=OE

在△CDO和△CEO中

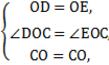
所以△CDO≌△CEO(SAS)

所以CD=CE

复习题第3题答案

解：因为OA=OB

所以∠A=∠B

又因为∠AOB=120°

所以∠A=∠B=1/2(180°-120°)=30°

过O作OC⊥AB,垂足为C

由垂径定理，得AC=CB=1/2AB

在Rt△ACO中，∠OCA=90°，∠A=30°，OA=20cm

所以OC=1/2OA=10（cm）

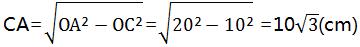
所以AB=2AC=30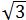(cm)

所以S△AOB=1/2AB•OC=1/2×20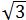×10=100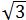(cm²)，即△AOB的面积是100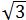cm²

复习题第4题答案

解：连接OC，则OC⊥AB

因为OA=OB

所以AC=CB=1/2AB

又因为AB=10cm

所以AC=CB=5cm

因为O的直径为8cm

所以OC=1/2×8=4(cm)

在Rt△AOC中，∠OCA=90〬，OC=4cm，AC=5cm

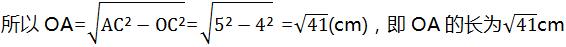
复习题第5题答案

解：过点E作EG⊥x轴，垂足为G,连接OE,则△OED是正三角形

∴∠EOG=60〬

∴∠OEG=30〬

又∵OE=2cm，∠OGE=90〬

∴OG=1/2OE=1cm

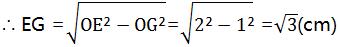
∴点E的坐标为（1，）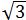

由题意知点D的坐标为（2，0）

结合正六边形的对称性可知A(-2，0)，B(-1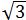，-)，C(1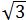，-)，F(-1，)

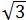故这个正六边形ABCDEF各个顶点的坐标分别为：

A(-2，0)，B(-1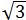，-)，C(1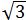，-)，D(2，0)，E(1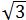，) ，F(-1，)

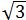复习题第6题答案

解：L₁和L₂的关系是L₁=L₂，理由如下：

设n个小半圆的直径分别为d1,d2,d3,…,dn,大半圆的直径为d大，则有d1+d2+d3+…+dn=d大

∴L2= 1/2(d1π+d2π+d3π+…+dnπ)= 1/2(d1+d2+d3+…+dn)π=1/2 d大π

又∵L₁= 1/2d大π

∴L₁=L₂

复习题第7题答案

解：由三角形内角和定理知∠A+∠B+∠C=180°,设∠A=α〬，∠B=β〬, ∠C=γ〬

∴α+β+γ=180°

∴S阴=(α×π×0.5²)/360+(β×π×0.52)/360+(γ×π×0.5²)/360

=(π×0.5²)/360（α+β+γ）

=(π×0.25)/360×180

=0.125π(cm²)

即阴影部分面积之和为0.125πcm²

复习题第8题答案

提示：找出三段弧所在圆的圆心即可

复习题第9题答案

解：点E,F,G,H四点共圆，圆心在点O处，理由如下：

连接HE,EF,FG, GH,OH, OE, OF, OG

∵E,F,G,H分别为AB,BC,CD,DA边上的中点

∴EF∥=1/2AC，HG∥=1/2AC

∴EF∥= HG

∴四边形EFGH是平行四边形

同时，由菱形ABCD的对角线互相垂直，可知：∠HEF=90〬

∴四边形EFGH是矩形

∴OH=OE=OF=OG

∴E,F,G,H四个点在同一个圆上，圆心为点O

复习题第10题答案

解：连接OA,过O作OC⊥AB，垂足为C,延长OC交O于点D

由垂径定理可知AC=CB=1/2AB=1/2×600=300(mm)

在Rt△OAC中，∠OCA=90〬，OA=1/2×650=325(mm)

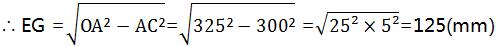
答：油的最大深度为200mm

复习题第11题答案

解：甲将球传给乙，让乙射门好，理由如下：如下图所示：

设AQ交O于点M 

连接PM,则∠B=∠PMQ

又因为∠PMQ是△PAM的一个外角,由外角性质，得∠PMQ>∠A

所以∠B>∠A

所以仅从射门角度考虑，甲将球传给乙，让乙射门好

复习题第12题答案

提示：可以证明“如果圆的两条切线互相平行，那么连接两切点所得线段是直径”，这就是利用图示方法可以测量圆的直径的道理.