习题24.3第1题答案
填表如下：
正多边形边数 | 内角 | 中心角 | 半径 |
| 3 | 60 | 120 | 2 |
| 4 | 90 | 90 |  |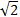
| 6 | 120 | 60 | 2 |
| 边长 | 边心距 | 周长 | 面积 |
2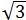 | 1 | 6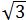 | 3 |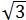
| 2 | 1 | 8 | 4 |
| 2 | 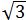 | 12 | 6 |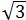
习题24.3第2题答案
解：如下图所示：
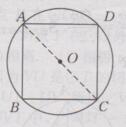
连接AC
∵∠D=90〬
∴AC为直径
在Rt△ACD中
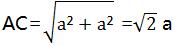
∴半径至少为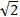
/2a
习题24.3第3题答案
解：正多边形都是轴对称图形
当正多边形的边数为奇数时，对称轴条数与正多边形边数相等，是正多边形顶点与对边中点所在的直线
当正多边形的边数为偶数时，它的对称轴条数也与边数相等，分别是对边中点所在的直线和相对顶点所在的直线.正多边形不都是中心对称图形
当正多边形边数为偶数时，它是中心对称图形，对称中心是正多边形的中心
当正多边形的边数为奇数时，它不是中心对称图形
习题24.3第4题答案
证明：∵ ABCDE为正五边形
∴ AB=BC=AE，∠A=∠B=∠C
又∵ L,H,I分别为AE,AB,BC边中点
∴ AL=AH=BH=BI=IC
∴ △AHL≌△BIH≌△CJI
∴ HL=HI=IJ，∠AHL=∠BHI=∠BIH=∠CIJ, ∠LHI=180°-∠AHL-∠BHI, ∠HIJ=180°-∠BIH-CIJ
∴∠LHI=∠HIJ
同理：LK=KJ=IJ=HI=HL, ∠HLK=∠LKJ=∠KJI=∠LHI=∠HIJ
∴五边形HIJKL是正五边形
习题24.3第5题答案
解：如下图所示：
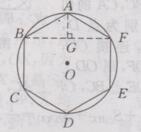
连接BF,过点A作AG⊥BF ,垂足为点G
因为∠BAF=120°
所以∠BAG=60°
所以∠ABG=∠30°
在Rt△ABG中，AB=12cm，∠AGB=90°，∠ABG=30°
所以AG=1/2AB=1/2×12=6（cm）
由勾股定理，得
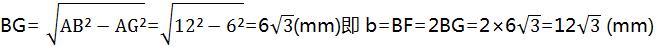
答：扳手张开的开口b至少要12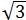
mm
习题24.3第6题答案
解：设剪去的小直角三角形的两直角边长分别为xcm，xcm,由题意可知（4-2x）2=x2+x2
解得x₁=4+2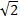
，x₂=4-2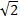
因为x<4
所以x=4+2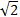
不符合题意，舍去
所以x=4-2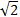
所以4-2x=4-2(4-2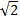
)=(4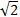
-4)cm,即这个正八边形的边长是(4
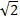-4)（cm）
S正八边形=S正方形-4S小三角形
=42-4×1/2•x•x
=16-2(4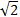-2
)2
=16-2 (24-16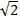
)
=（32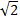
-32）cm2
答：这个正八边形的边长为(4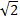
-4)cm，面积是（32
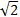-32）cm2
习题24.3第7题答案
解：①当用48cm长的篱笆围成一个正三角形时，边长为48÷3=16（m）,此时 S△=1/2×16×8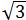
=64
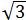（m2）
②当围成一个正方形时，边长为48÷4=12（m），此时S正方形=12×12=144（m2）
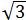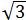③当围成一个正六边形时，边长为48÷6=8（m),此时S正六边形=6×1/2 ×8×4=96（m2）
④当围成一个圆时，圆的半径为48/2π=24/π（m）,此时，S圆=π（24/π）2=576/π（m2）
因为64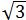
<144<96
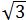<576/π
所以S圆最大
答：用48cm长的篱笆围成一个圆形的绿化场地面积最大
习题24.3第8题答案
提示：圆外切正三角形的边长为2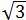
R；圆外切正四边形的边长为2R；圆外切正六边形的边长为(2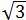)/3R
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
译林牛津版九年级下册英语课本答案
九年级上册语文课课练答案苏教版
鲁教版化学书九年级下册答案
九年级上册语文同步练习答案苏教版
九年级上册译林版英语同步练习答案
九年级思想品德新编基础训练答案人教版
九年级下册思想品德课课练答案苏人版
人教版九年级下册语文南方新课堂答案
上教版九年级上册化学补充习题答案
人教版九年级上册数学新课程自主学习与测评答案