习题24.2第1题答案
（1）点P在O内
（2）点P在O上
（3）点P在O外
习题24.2第2题答案
【提示】
（1）相离
（2）相切
（3）相交
习题24.2第3题答案
（1）因为VU是T的切线，U为切点
所以UT⊥UV
所以∠VUT=90〬°
在Rt△UVT中，∠UVT=90〬°,UV=28cm， TU=25cm
所以VT2=UV2+TU2,即VT2=282+252
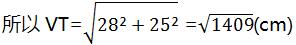
（2）因为VU与VW均是T的切线
所以∠UVT=∠TVW，∠TWV=90〬°
又因为∠UVW=60°
所以∠TVW=1/2×60=30°
在Rt△TVW中，∠TWV=90〬°，∠TVW =30°，TW=25cm
所以TV=2WT=2×25=50（cm）
习题24.2第4题答案
证明：连接OC
∵OA=OB
∴△OAB为等腰三角形
又∵CA=CB
∴OC⊥AB
∵AB经过O的半径OC的外端C，并且垂直于半径OC
∴AB是O的切线
习题24.2第5题答案
证明：连接OP，因为AB是小圆O的切线，P为切点
所以OP⊥AB
又AB是大圆O的弦
所以由垂径定理可知AP=PB
习题24.2第6题答案
解：因为PA，PB是O的切线
所以PA=PB，∠PAB=∠PBA
又由题意知OA⊥PA，∠OAB=25〬°
所以∠PAB=90〬°-25〬°=65〬°
所以∠P=180〬°-2∠PAB=180〬°-65〬°×2=50〬°
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级上册物理配套练习册答案人教版
浙教版九年级下册数学课本答案
沪粤版九年级下册物理作业本答案江西省
九年级下册化学书答案上教版
九年级下册数学同步练习答案沪科版
九年级下册历史课时练答案人教版
九年级下册数学同步训练答案人教版
九年级下册科学作业本答案浙教版