习题24.1第13题答案
证明：连接OC
∵C是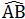
的中点
∴
∴∠AOC=∠BOC
又∵∠AOB=120〬
∴∠AOC=∠BOC=1/2×120〬=60〬
又∵OA=OC=OB
∴△AOC与△BOC均是等边三角形
∴OA=AC=OC, BO=OC=BC
∴OA=AC=BC=OB
∴四边形OACB是菱形
习题24.1第14题答案
解：△ABC是等边三角形，证明如下：
∵∠APC=∠CPB=60〬
∴∠BAC=∠ABC=60〬
∵∠ACB=180〬-∠BAC-∠ABC=180〬-60〬-60〬=60〬
∴∠ABC=∠ACB=∠BAC
∴AB=BC=CA
∴△ABC是等边三角形
习题24.1第15题答案
解：OM<ON，理由如下：如下图所示：
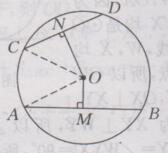
连接OC,OA,则OA=OC
∵ON⊥CD,OM⊥AB
∴CN=1/2CD,AM=1/2 AB
又∵CD<AB
∴CN<AM
∴CN2<AM2
在Rt△OCN和Rt△OAM中，OM2=OA2-AM2, ON2=OC2-CN2
∴OM2<ON2
∴OM<ON
习题24.1第16题答案
解：如下图所示：
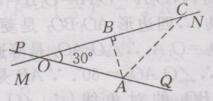
过点A作AB⊥ON,垂足为B
因为∠QON=30〬，OA=200m，∠OBA=90〬
所以AB=1/2OA=1/2×200=100(m)
因为100m<200m
所以居民楼会受到噪音的影响
在MN上找到点C，使AC=200m，又OA=200m，则火车在铁路MN上沿ON方向行驶到点O处时，居民楼开始受到火车噪音的影响
由勾股定理，得OB2=OA2-AB2=2002-1002=30000
所以OB=100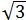
（m）,同理BC=100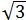（m）
所以OC=OB+BC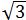=100
+100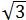
=200
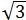（m）
又（200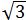
÷1000）÷72×3600=10
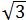≈17.3（s）
所以居民楼受噪音影响的时间约为17.3s
习题24.1第17题答案
同弧所对的圆外角小于相应地圆周角，因此只要航行中保持∠XPY<∠XZY，就能保证点P在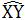
所在的圆外，也就保证了船只不进入浅滩
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级上册思想品德课课练答案苏人版
九年级上册化学学法大视野答案人教版
人教版九年级下册历史知识与能力训练答案
人教版九年级上册化学作业本答案江西省
浙教版九年级下册数学课本答案
九年级下册数学同步练习答案苏科版
九年级下册历史新课程自主学习与测评答案人教版
苏科版九年级上册数学书答案
九年级下册化学新编基础训练答案人教版