习题24.1第7题答案
已知：如下图所示：
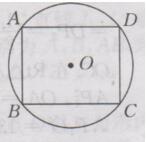
四边形ABCD为⨀O内接平行四边形
求证：◇ABCD为矩形.
证明：四边形ABCD为平行四边形
∴∠A=∠C
又∵四边形ABCD内接于O
∴∠A+∠C=180〬
∴∠A=∠C=90〬
∴◇ABCD为矩形
习题24.1第8题答案
解：如下图所示：
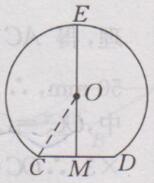
连接OC，设O的半径为r
∵M为CD的中点
∴OM⊥CD
∴CM=1/2CD=1/2×4=2cm
在Rt△CMO中，OC2-OM2=CM2，即r2-(6-r)2=22, r2-(36-12r+ r2)=4，12r=40，r=10/3
∴O的半径为10/3 cm
习题24.1第9题答案
证明：如下图所示：
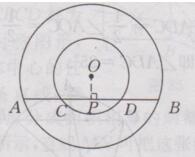
过点O作OP⊥AB，垂足为点P
由垂径定理可知PA=PB，PC=PD
∴PA-PC=PB-PD，即AC=BD.
习题24.1第10题答案
解：分两种情况讨论.①当AB、CD在点O的同侧时，如下图所示：
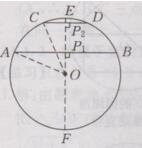
过点O作EF⊥AB，垂足为P₁，交O于点E、F，交CD于P₂
∵CD//AB
∴CD⊥EF，由垂径定理可知AP₁=BP₁=1/2AB=24×1/2=12(cm)
CP₂=DP₂=1/2CD=5(cm)
连接OA，OC
在Rt△AOP₁中，P₁O2=OA2-AP₁2，OA=13cm，AP₁=12cm
∴P₁O2=132-122=25
∴P₁O=5cm，同理
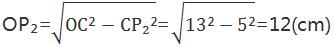
∴P₁P₂=OP₂-OP₁=12-5=7（cm）
②当AB、CD在点O的两侧时，如下图所示：
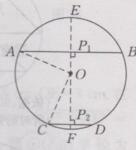
与AB、CD在点O的同侧时的解法类似，可得OP₁=5cm， OP₂=12cm
∴P₁P₂=OP₁+OP₂=5+12=17(cm) , 即AB与CD的距离为7cm或17cm
习题24.1第11题答案
证明：∵AB//CD，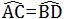
又∵MN是AB的垂直平分线，则有,MN过圆心O，是直径
∴
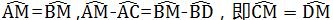
∴MN垂直平分CD
习题24.1第12题答案
∵OC⊥AB,AB=300
∴由垂径定理，可知AD=DB=1/2AB=150
又∵CD=45
∴OD=OC-CD=OC-45
又∵OA,OC均为O的半径
∴OA=OC
在Rt△AOD中，OA2=OD2+AD2
∴OC2=(OC-45)2+1502
∴OC=272.5（m）
答：这段弯路的半径是272.5m
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级上册思想品德课课练答案苏人版
九年级上册化学学法大视野答案人教版
人教版九年级下册历史知识与能力训练答案
人教版九年级上册化学作业本答案江西省
浙教版九年级下册数学课本答案
九年级下册数学同步练习答案苏科版
九年级下册历史新课程自主学习与测评答案人教版
苏科版九年级上册数学书答案
九年级下册化学新编基础训练答案人教版