习题24.1第1题答案
已知：如下图所示：
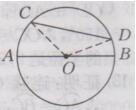
在O中，AB为直径，CD为O的任意一条弦（不是直径的弦）
求证：AB>CD
证明：连接OC,OD，在△OCD中，OC+OD>CD,即AB>CD
习题24.1第2题答案
（1）∵OA,OB是O的半径
∴OA=OB=50mm
又∵AB=50mm
∴OA=OB=AB
∴△AOB是等边三角形
∴∠AOB=60〬
（2）过点O作OC⊥AB,垂足为点C，如下图所示：
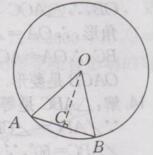
则∠OCA=90〬，由垂径定理得，AC=CB=1/2AB
∵AB=50mm
∴AC=25mm
在Rt△OAC中，OC2=OA2-AC2=502-252=252×3
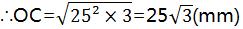
即点O到AB的距离是25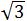
mm
习题24.1第3题答案
解：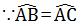
∴AB=AC
∴∠B=∠C=75〬
∴∠A=180〬-75〬-75〬=30〬，即∠A的度数是30〬
习题24.1第4题答案
解：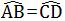
,证明如下：
∵AD=BC,
∴
∴
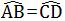
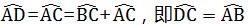
习题24.1第5题答案
解：如下图所示：
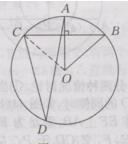
连接OC
∵OA⊥BC
∴
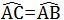
∴∠COA=∠AOB
∵∠AOB=50〬
∴∠COA=50〬
∴∠ADC=1/2∠AOC=1/2×50〬=25〬，即∠ADC=25〬
习题24.1第6题答案
解：第二个（即中间的）工件是合格的，理由是90〬°的圆周角所对的弦是直径
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级上册思想品德课课练答案苏人版
九年级上册化学学法大视野答案人教版
人教版九年级下册历史知识与能力训练答案
人教版九年级上册化学作业本答案江西省
浙教版九年级下册数学课本答案
九年级下册数学同步练习答案苏科版
九年级下册历史新课程自主学习与测评答案人教版
苏科版九年级上册数学书答案
九年级下册化学新编基础训练答案人教版