习题1.6第1题答案
解:在矩形ABCD中,AC=BD=4,∠ABC=90°,∠ACB=30°
∴AB= 1/2 AC= 1/2×4=2
在Rt△ABC中,由勾股定理,得
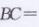
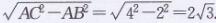
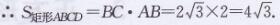
习题1.6第2题答案
解:在矩形ABCD中,∠BAD=90°,即∠BAE+∠EAD=90°
∵∠EAD=3∠BAE
∴∠BAE+3∠BAE=90°,∠BAE=22.5°
∴∠EAD=3∠BAE=3×22.5°=67.5°
∵AE⊥BO
∴∠AEB=90°
∴∠BAE+∠ABE=90°,即22.5°+∠ABE=90°
∴∠ABE=67.5°
∵AC=BC,OA=1/2 AC,OB= 1/2 BD
∴OA=OB
∴∠OAB=∠ABE=67.5°
∵∠EAO+∠BAE=∠OAB
∴∠EAO=∠OAB-∠BAE=67.5°-22.5°=45°
习题1.6第3题答案
证明:∵D是BC的中点
∴BD=CD
∵四边形ABDE是平行四边形
∴AE//BC,AE=BD,ED=AB(平行四边形的性质)
∴AE=CD
∵AE//CD
∴四边形ADCE是平行四边形(一组对边平行且相等的平行四边形是矩形)
∵AB=AC
∴ED=AC
∴平行四边形ADCE是矩形(一组对边平行且相等的四边形是平行四边形)
习题1.6第4题答案
解:将矩形纸片ABCD折叠,使点C与点A重合得到的图形如下图所示:
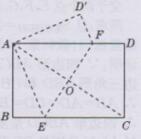
折痕为EF,则AE=CE,EF垂直平分AC,连接AC交EF于点O
在矩形ABCD中,∠B=90°,BC=8cm
设CE=x cm,则AE=x cm,BE=BC-CE=(8-x)cm
在Rt△ABE中,由勾股定理,得AE2=AB2+BE2,X2=62+(8-x)2
解得x=25/2,即EC=25/4cm
在Rt△ABC中,由勾股定理,得
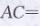
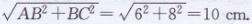
∴OC=1/2=AC=1/2×10=5cm
∵EF⊥AC
∴∠EOC=90°
在Rt△EOC中,由勾股定理,得EO2=EC2-OC2
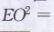
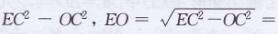
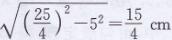
∴折痕EF=2EO=2×15/4=15/2 cm
习题1.6第5题答案
解:如下图所示:
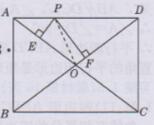
连接PO,S矩形ABCD=AB·BC=3×4=12
在Rt△ABC中:
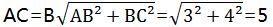
又因为AC=BD,AO=1/2 AC,DC=1/2 BD
所以AO=DO=5/2
所以S△AOD=S△APO+S△POD=1/2 AO·PE+ 1/2 DO∙PE= 1/2 AO(PE+PE)=1/2×5/2(PE+PE)=5/4(PE+PE)
又因为S△AOD=1/4S矩形ABCD=1/4×12=3
所以5/4(PE+PE)=3
解得PE+PE=12/5

 九年级上册化学课本答案沪教版
九年级上册化学课本答案沪教版 华东师大版九年级上册数学书答案
华东师大版九年级上册数学书答案 人教版九年级上册化学书答案
人教版九年级上册化学书答案 人教版九年级上册物理书答案
人教版九年级上册物理书答案 人教版九年级上册英语书答案
人教版九年级上册英语书答案 浙教版九年级上册科学书答案
浙教版九年级上册科学书答案 沪科版九年级上册数学书答案
沪科版九年级上册数学书答案 浙教版九年级上册数学书答案
浙教版九年级上册数学书答案 人教版九年级上册语文书答案
人教版九年级上册语文书答案 北师大版九年级上册数学书答案
北师大版九年级上册数学书答案 沪教版化学书九年级下册答案
沪教版化学书九年级下册答案 九年级下册科学作业本答案浙教版
九年级下册科学作业本答案浙教版 九年级上册英语学法大视野答案人教版
九年级上册英语学法大视野答案人教版 九年级上册思想品德课课练答案苏人版
九年级上册思想品德课课练答案苏人版 九年级下册历史新课程自主学习与测评答案人教版
九年级下册历史新课程自主学习与测评答案人教版 九年级下册语文作业本答案人教版
九年级下册语文作业本答案人教版 北师大版数学书九年级下册答案
北师大版数学书九年级下册答案 人教版九年级下册物理配套练习册答案
人教版九年级下册物理配套练习册答案 九年级下册化学同步解析与测评答案人教版
九年级下册化学同步解析与测评答案人教版 九年级下册化学长江作业本答案人教版
九年级下册化学长江作业本答案人教版