习题1.5第1题答案
（1）四边形ABCD是平行四边形（对角线互相平分的四边形是平行四边形）
（2）当△ABC是直角三角形，即∠BAC=90°时，四边形ABEC是矩形
习题1.5第2题答案
解：四边形ACBD是矩形.证明如下：
如下图所示：
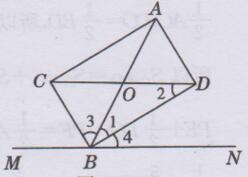
∵CD//MN
∴∠2=∠4
∵BD平分∠ABN
∴∠1=∠4
∴∠1=∠2
∴OB=OD（等角对等边）
同理可证OB=OC
∴OC=OD
∵O是AB的中点
∴OA=OB
∴四边形ACBD是平行四边形（对角线互相平分的四边形是平行四边形）
又∵BC平分∠ABM
∴∠3=1/2∠ABM
∵BD平分∠ABN
∴∠1= 1/2∠ABN
∵∠ABM+∠ABN=180°
∴2∠3+2∠1=180°
∴∠3+∠1=90°，即∠CBD=90°
∴平行四边形ACBD是矩形（有一个角是直角的平行四边形是矩形）
习题1.5第3题答案
解：做法如下：如下图所示：
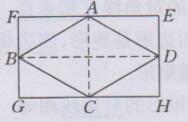
（1）连接AC,BD
（2）过A,C两点分别作EF//BD,GH//BD
（3）同法作FG//AC,EH//AH,与EF,GH交于四个点E，F,G,H,则矩形EFGH即为所求，且S矩形EFGH=2S菱形ABCD
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级上册思想品德课课练答案苏人版
九年级下册英语同步解析与测评答案人教版
九年级上册英语课课练答案译林版
九年级下册科学课时特训答案浙教版
九年级下册思想品德新课程自主学习与测评答案人教版
苏科版九年级上册数学书答案
教科版九年级下册物理作业本答案江西省
九年级上册数学阳光学业评价答案人教版
九年级上册译林版英语同步练习答案
九年级下册历史新课程自主学习与测评答案人教版