习题1.3第1题答案
证明：
（1）∵四边形ABCD是菱形
∴AD=CD,AB=CB,∠A=∠C
∵BE=BF
∴AB-BE=CB-BF,即AE=CF
在△ADE和CDF中
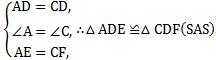
（2）∵△ADE≌△CDF
∴DE=DF
∴∠DEF=∠DFE（等边对等角）
习题1.3第2题答案
已知：如下图所示：
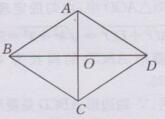
四边形ABCD是菱形，AC和BD是对角线
求证：S菱形ABCD=1/2 AC∙BD
证明：∵四边形ABCD是菱形
∴AC⊥BD,AO=CO,BO=DO
∴S△AOB=S△AOD=S△BOC=S△COD=1/2 AO·BO
∴S菱形ABCD=4×1/2 AO∙BO= 1/2×2AO∙2BO=1/2 AC∙BD
习题1.3第3题答案
解：在菱形ABCD中，AC⊥BD
∴∠AOB=90°，AO= 1/2 AC= 1/2×16=8，BO= 1/2 BD= 1/2×12=6
在Rt△AOB中，由勾股定理，得AB=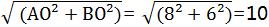
∵S菱形ABCD=1/2 AC∙BD= 1/2×16×12=96
又∵DH⊥AB
∴S菱形ABCD=AB∙DH
∴96=AB∙DH,即96=10DH,DH=9.6
∴菱形ABCD的高DH为9.6
习题1.3第4题答案
证明：∵点E,F,G,H分别是AB,CD,AC,BD,的中点
∴GF是△ADC的中位线，EH是△ABD的中位线
∴GF//AD,GF=1/2 AD,EH//AD,EH=1/2AD
∴GF//EH,GF=EH
∴四边形EGFH是平行四边形（一组对边平行且相等的四边形是平行四边形）
又∵FH是△BDC的中位线
∴FH=1/2 BC
又∵AD=BC
∴GF=FH
∴平行四边形EGFH是菱形（一组邻边相等的平行四边形是菱形）
习题1.3第5题答案
提示：折叠过程中要依据菱形的判定定理
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级下册思想品德长江作业本答案人教版
华东师大版数学书九年级下册答案
九年级下册英语同步解析与测评答案人教版
人教版九年级下册化学配套练习册答案
九年级下册数学长江作业本答案人教版
九年级下册语文同步练习答案苏教版
九年级下册数学书答案华东师大版
九年级上册数学配套练习册答案青岛版
九年级上册语文学法大视野答案北师大版
物理九年级下册学习与评价答案苏科版