习题1.1第1题答案
证明：∵四边形ABCD是菱形
∴BC=AB,BC//AD
∴∠B+∠BAD=180°（两直线平行，同旁内角互补）
∵∠BAD=2∠B
∴∠B+2∠B=180°
∴∠B=60°
∵BC=AB
∴△ABC是等边三角形（有一个角为60°的等腰三角形的等边三角形）
习题1.1第2题答案
解：∵四边形ABCD是菱形
∴AD=DC=CB=BA
∴AC±BD,AO=1/2 AC= 1/2×8=4，DO= 1/2 BD= 1/2×6=3
在Rt△AOD中
由勾股定理，得AD=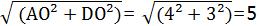
∴菱形ABCD的周长为4AD=4×5=20
习题1.1第3题答案
证明：∵四边形ABCD是菱形
∴AD=AB,AC±BD，DO=BO
∴△ABD是等腰三角形
∴AO是等腰△ABD低边BD上的高，中线，也是∠DAB的平分线
∴AC平分∠BAD
同理可证AC平分∠BCD,BD平分∠ABC和∠ADC
习题1.1第4题答案
有4个等腰三角形和4个直角三角形
推荐阅读
九年级上册化学课本答案沪教版
年级：九年级
版本：沪教版
科目：化学
学期：上册
名称：课本
华东师大版九年级上册数学书答案
年级：九年级
版本：华东师大版
科目：数学
学期：上册
名称：课本
人教版九年级上册化学书答案
年级：九年级
版本：人教版
科目：化学
学期：上册
名称：课本
人教版九年级上册物理书答案
年级：九年级
版本：人教版
科目：物理
学期：上册
名称：课本
人教版九年级上册英语书答案
年级：九年级
版本：人教版
科目：英语
学期：上册
名称：课本
浙教版九年级上册科学书答案
年级：九年级
版本：浙教版
科目：科学
学期：上册
名称：课本
沪科版九年级上册数学书答案
年级：九年级
版本：沪科版
科目：数学
学期：上册
名称：课本
浙教版九年级上册数学书答案
年级：九年级
版本：浙教版
科目：数学
学期：上册
名称：课本
人教版九年级上册语文书答案
年级：九年级
版本：人教版
科目：语文
学期：上册
名称：课本
北师大版九年级上册数学书答案
年级：九年级
版本：北师大版
科目：数学
学期：上册
名称：课本
九年级上册数学学法大视野答案湘教版
年级：九年级
版本：湘教版
科目：数学
学期：上册
名称：学法大视野
华东师大版数学书九年级下册答案
年级：九年级
版本：华东师大版
科目：数学
学期：下册
名称：课本
人教版九年级上册物理书答案
年级：九年级
版本：人教版
科目：物理
学期：上册
名称：课本
译林版英语书九年级下册答案
年级：九年级
版本：译林版
科目：英语
学期：下册
名称：课本
人教版九年级上册思想品德作业本答案
年级：九年级
版本：人教版
科目：思想品德
学期：上册
名称：作业本
九年级下册数学配套练习册答案青岛版
年级：九年级
版本：青岛版
科目：数学
学期：下册
名称：配套练习册
沪粤版物理书九年级下册答案
年级：九年级
版本：沪粤版
科目：物理
学期：下册
名称：课本
人教版九年级下册语文南方新课堂答案
年级：九年级
版本：人教版
科目：语文
学期：下册
名称：南方新课堂
九年级上册数学配套练习册答案青岛版
年级：九年级
版本：青岛版
科目：数学
学期：上册
名称：配套练习册
九年级上册语文课课练答案苏教版
年级：九年级
版本：苏教版
科目：语文
学期：上册
名称：课课练