习题13.3第7题答案
解：∵AB=AC，∠=40°
∴∠ABC=∠C=1/2×（180°-40°）=70°
又∵MN是AB的垂直平分线
∴DA=DB
∴∠A=∠ABD=40°
∴∠DBC=∠ABC-∠ABD=70°-40°=30°
习题13.3第8题答案
已知：如下图所示：
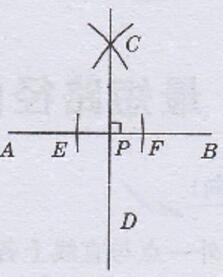
点P是直线AB上一点，求作直线CD，使CD⊥AB于点P
作法：
(1)以点P为圆心作弧交AB于点E，F
(2)分别以点E，F为圆心，大于1/2EF的长为半径作弧，两弧相交于点C，过C，P作直线CD，则直线CD为所求直线
习题13.3第9题答案
解：他们的判断是对的
理由：因为等腰三角形底边上的中线和底边上的高重合
习题13.3第10题答案
证明：∵BO平分∠ABC
∴∠MBO=∠CBO
∵MN∥BC
∴∠BOM=∠CBO
∴∠BOM=∠MBO
∴BM=OM
同理CN=ON
∴AM+MN+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC
即△AMN的周长等于AB+AC
习题13.3第11题答案
解：∵∠NBC=84°，∠NAC=42°，∠MBC=∠NAC+∠C即84°=42°+∠C
∴∠C=42°
∴BC=BA
又∵BA=15×（10-8）=30（n mile）
∴BC=30n mile，即从海岛B到灯塔C的距离是30n mile
习题13.3第12题答案
证明：∵△ABD，△AEC都是等边三角形
∴AD=AB，AC=AE，∠DAB=∠EAC=60°
∴∠DAB+∠BAC=∠EAC+∠BAC，即∠DAC=∠BAE
在△ADC和△ABE中
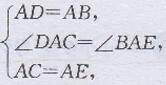
∴△ADC≌△ABE（SAS）
∴BE=DC
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
八年级下册语文新课程自主学习与测评答案人教版
八年级下册生物同步解析与测评答案人教版
八年级下册数学同步训练答案人教版
八年级上册语文配套练习册答案人教版
八年级下册语文南方新课堂答案人教版
八年级下册思想品德新编基础训练答案人教版
八年级下册数学作业本答案浙教版
人教版八年级上册英语作业本答案江西省
八年级下册语文作业本答案人教版
人教版八年级下册语文作业本答案江西省