复习题11第7题答案
解：∵∠C+∠ABC+∠A=180°
∴∠C+∠C+1/2∠C=180°
解得∠C=72°
又∵BD是AC边上的高
∴∠BDC=90°
∴∠DBC=90°-72°=18°
复习题11第8题答案
解：∠DAC=90°-∠C= 20°
∠ABC=180°-∠C-∠BAC=60°
又∵AE，BF是角平分线
∴∠ABF=1/2∠ABC=30°，∠BAE=1/2∠BAC=25°
∴∠AOB=180°-∠ABF-∠BAE=125°
复习题11第9题答案
BD；PC；BD+PC；BP+CP
复习题11第10题答案
解：因为五边形ABCDE的内角都相等
所以∠B=∠C=((5-2)×180°)/5=108°
又因为DF⊥AB
所以∠BFD=90°
在四边形BCDF中，∠CDF+∠BFD+∠B+∠C=360°
所以∠CDF=360°-∠BFD-∠B-∠C=360°-90°-108°-108°=54°
复习题11第11题答案
证明：(1)如下图所示：
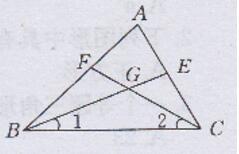
因为BE和CF是∠ABC和∠ACB的平分线
所以∠1=1/2∠ABC，∠2=1/2∠ACB
因为∠BGC+∠1+∠2 =180°
所以BGC=180°-（∠1+∠2）=180°-1/2（∠ABC+∠ACB）
(2)因为∠ABC+∠ACB=180°-∠A
所以由(1)得，∠BGC=180°-1/2(180°-∠A)=90°+1/2∠A
复习题11第12题答案
证明：在四边形ABCD中
∠ABC+∠ADC+∠A+∠C=360°
因为∠A=∠C=90°
所以∠ABC+∠ADC= 360°-90°-90°=180°
又因为BE平分∠ABC，DF平分∠ADC
所以∠EBC=1/2∠ABC, ∠CDF=1/2∠ADC
所以∠EBC+∠CDF=1/2（∠ABC+∠ADC）=1/2×180°=90°
又因为∠C=90°
所以∠DFC+∠CDF =90°
所以∠EBC=∠DFC
所以BE//DF
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
八年级下册生物同步导学与优化训练答案人教版
八年级下册英语长江作业本答案人教版
八年级上册语文同步解析与测评答案人教版
八年级下册物理同步解析与测评答案人教版
八年级上册生物学法大视野答案苏教版
八年级下册数学南方新课堂答案人教版
人教版八年级上册英语作业本答案
八年级下册数学课时作业本答案人教版
苏教版八年级上册思想品德补充习题答案