第六章复习题第15题答案
解:∠BED=∠ABC.理由如下:
在Rt△ACD与Rt△CED中,
∵∠ACD=∠CED,∠ADC=∠CDE,
∴Rt△ACD∽ Rt△CED.
∴AD/CD=CD/ED .
∵CD=BD,∴AD/BD=BD/ED .
在△ABD和△BED中,
∵∠ADB=∠BDE,AD/BD=BD/ED,
∴△ABD∽△BED.
∴∠BED=∠ABC.
第六章复习题第16题答案
解:△AEF∽△ECF.理由如下:
∵CE⊥EF,
∴∠FEC= 90°.
∴∠AEF+ ∠DEC=90°.
又∵∠AEF+∠AFE= 90°,
∴∠DEC=∠AFE.
在Rt△AEF与Rt△DCE中,
∠AFE=∠DEC,∠A=∠D,
∴Rt△AEF∽Rt△DCE.
∴AE/DC=EF/CE .
又∵AE=ED,∴ED/EC=EF/(C E),即ED/EF=DC/CE .
又∵∠FEC=∠D,
∴Rt△DCE∽Rt△ECF.
∴Rt△AEF∽Rt△ECF.
第六章复习题第17题答案
解:(1)A1(1,3),O1(一1,0),B1(2,0);
(2)A2(-2,-3),B2(-3,0);
(3)A3(2,-3);
(4)A4(4,6),B4(6,0)或A4(-4,-6),B4(一6,0).
第六章复习题第18题答案
解:由AC=1.5 m,△ABC的面积为1.5 m2,得BC=2m
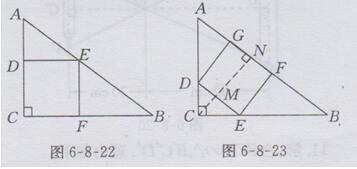
如图6-8-22所示,设甲加工的桌面边长为xm.
由DE∥CB,AD/AC=DE/CB,
即(1.5-x)/1.5=x/2,解得x=6/7.
如图6-8-23所示,过点C作CN ⊥AB,分别交DE、AB于点M、N.
在Rt△ABC中,由AC=1.5 m,BC=2m,
△ABC的面积为1.5 m2,得AB=2.5m,CN=1.2m.
设乙加工的桌面边长ym,
由DE∥AB,得DE/AB=CM/CN,
即y/2.5=(1.2-y)/1.2,解得y=30/37 .
因为x>y,所以甲同学的加工方法符合要求.
第六章复习题第19题答案
解:能.
步骤一:过点C′作直线与A′B′相交于点D',使∠A′C′D′=∠B;
步骤二:过点C作直线与AB相交于点D,使∠BCD=∠A’.
由作图可知:△BCD∽△C′A'D’
由∠ACD+∠BCD=90°,∠A′+∠B′=90°,∠BCD=∠A’,
得∠ACD=∠B’,
由∠ADC=∠B+∠BCD.∠B′D′C=∠A′+∠A′C′D′,
得∠ADC=∠B'D'C'.
由此得△ACD∽△C′B'D’.
第六章复习题第20题答案
解:AE/AC=1/(2n+1) .理由如下:
如图6-8-24所示,
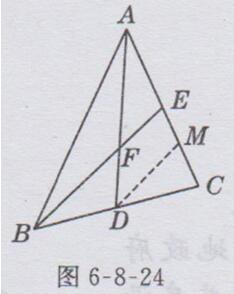
过点D作DM//BE.
∵D是BC的中点,
∴M是EC的中点.
∵DM//BE,
∴△AFE∽△ADM.
∴AF/AD=AE/AM .
∵AE/AM=2AE/(AC+AE),
∴AE/AD=2AE/(AC+AE),即1/(n+1)=2AE/(AC+AE),
整理,得AC=(2n+1)AE.
∴AE/AC=1/(2n+1) .
第六章复习题第21题答案
解:(1)当D是AB的中点时,E也是AC的中点,
∴AE=EC,
∴S′=S△ADE.
∵DE∥BC,∴△ADE∽△ABC.
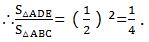
∴S'/S=1/4 .
(2).∵DE∥BC,∴当AD=x时,
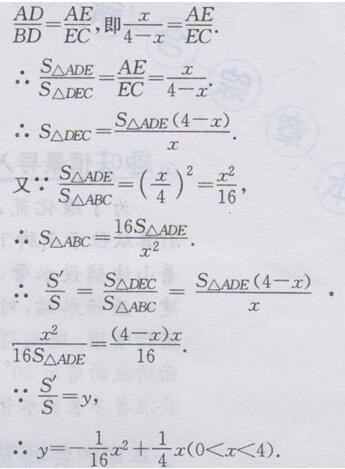
(3)由(2)知y=-1/16x2+1/4x=-1/16(x-2)2+1/4,
∴0<y≤1/4,∴0<S'/S≤1/4 .∴S′<S

 鲁教版语文书九年级下册答案
鲁教版语文书九年级下册答案 北师大版数学书九年级下册答案
北师大版数学书九年级下册答案 人教版语文书九年级下册答案五四制
人教版语文书九年级下册答案五四制 华东师大版数学书九年级下册答案
华东师大版数学书九年级下册答案 苏科版数学书九年级下册答案
苏科版数学书九年级下册答案 湘教版数学书九年级下册答案
湘教版数学书九年级下册答案 鲁教版数学书九年级下册答案五四制
鲁教版数学书九年级下册答案五四制 译林版英语书九年级下册答案
译林版英语书九年级下册答案 沪教版英语书九年级下册答案
沪教版英语书九年级下册答案 外研版英语书九年级下册答案
外研版英语书九年级下册答案 九年级下册数学课时作业本答案人教版
九年级下册数学课时作业本答案人教版 译林牛津版九年级下册英语课本答案
译林牛津版九年级下册英语课本答案 华东师大版九年级上册数学书答案
华东师大版九年级上册数学书答案 教科版九年级上册物理作业本答案江西省
教科版九年级上册物理作业本答案江西省 九年级下册数学配套练习册答案人教版
九年级下册数学配套练习册答案人教版 人教版九年级上册英语作业本答案
人教版九年级上册英语作业本答案 九年级下册物理长江作业本答案人教版
九年级下册物理长江作业本答案人教版 九年级下册历史课时练答案人教版
九年级下册历史课时练答案人教版 九年级下册数学作业本答案浙教版
九年级下册数学作业本答案浙教版 人教版九年级上册英语作业本答案江西省
人教版九年级上册英语作业本答案江西省