习题5.5第1题答案
解：把h=55代入h=4. 9t2，得55=4 9t2．解得t=士3.4．
∵t=-3.4不符合题意，舍去．
∴t=3.4
答：试验物大约经过3.4 s落地．
习题5.5第2题答案
解：把t=1.3 s代入h=4. 9t2，
得h=4. 9×1.32，解得h=4.9×1.32≈8.3(m)．
答：该枯井大约有8.3 m深．
习题5.5第3题答案
解：设长方形生物园的长为xm，面积为y m2，则y=x（(16-2x)/2）=-x2+ 8x=-（x-4）2+16．
∴当x=4时，y的值最大
∴长方形的生物园的长与宽相等，都等于4m时，小兔的活动范围最大.
习题5.5第4题答案
解：设每辆汽车月租费增加x元，月收益为y元，则
y=（100-1/50x）（3000+x）-200（100-1/50x）
=-1/50（x-1100）2+304200.
当x=1100时，y值最大.
即每月租出100-1/50×1100=78辆汽车时，收益最大，最大收益为304200元.
习题5.5第5题答案
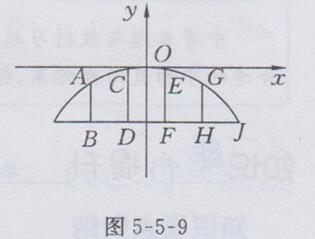
解：建立如图5-5-9所示的平面直角坐标系
设所求函数表达式为y=ax2(a≠o)．
∵此函数图像过点J（1，-0.5)，
将（1，-0.5）代人y=ax2，得a= -0.5，
即抛物线的函数表达式为y= -0.5x2．
将x=0.2代人y= -0.5x2，得y=-0. 02
∴E点的坐标为(0.2，-0. 02).
同理，求得G点的坐标为(0.6，-0. 18)．
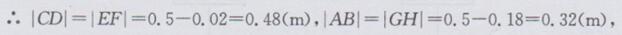
∴四条立柱总长为（0.48+0.32）×2=1.6（m），∴共需钢管1.6×50=80（m）.
习题5.5第6题答案
解：（1）建立如图5-5-14所示的平面直角坐标系，设二次函数的表达式为y=ax2，拱桥最高点O到水面CD的距离为h米，则D（5，-h），B（10，-h-3）.
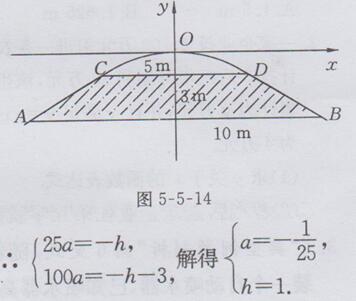
∴二次函数的表达式为y=-1/25x2.
（2）当x=5时，y=-1/25×25=-1，
∴t=1/0.2=5（h），
即再过5h此桥孔将会被淹没.
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册历史新课程自主学习与测评答案人教版
九年级上册英语学法大视野答案人教版
英语九年级上册学习与评价答案译林版
九年级上册语文学法大视野答案人教版
人教版九年级上册化学新课程自主学习与测评答案
沪教版化学书九年级下册答案
浙教版九年级上册数学课时特训答案
人教版九年级上册语文作业本答案
数学九年级上册轻轻松松学数学冀教版
人教版九年级上册思想品德作业本答案