习题2.5第1题答案
解：（1）开口向上，对称轴为直线x=2，顶点坐标为（2,5）。
（2）方法1（配方法）：
∵y=2x2-4x-1=2（x-1）2-3
∴图像开口向上，对称轴为直线x=1，顶点坐标为（1，-3）.
方法2（公式法）：
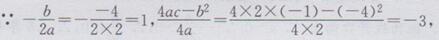
∴图像开口向上，对称轴为直线x=1，顶点坐标为（1，-3）.
（3）方法1（配方法）：
∵y=3x2-6x+2=3（x-1）2-1，
∴图像开口向上，对称轴为直线x=1，顶点坐标为（1，-1）.
方法2（公式法）：
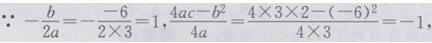
∴图像开口向上，对称轴为直线x=1，顶点坐标为（1，-1）.
（4）原函数的表达式变为y=-3x2-36x-81，开口向下，
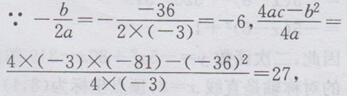
∴对称轴为直线x=-6，顶点坐标为（-6，27）.
习题2.5第2题答案
解：y=x2-2x+1=（x-1）2，将二次函数y=x2-2x+1的图像向上平移2个单位，再想做平移3个单位长度，得到y=（x-1+3）2+2，即y=（x+2）2+2.整理，得y=x2+4x+6.有题意可知y=x2+bx+c，所以x2+4x+6=x2+bx+c，可得b=4，c=6.因为二次函数的表达式为y=（x+2）2+2，所以抛物线开口向上，对称轴为直线x=-2，顶点坐标为（-1,2）。草图略。
习题2.5第3题答案
解：∵a=-5<0，
∴抛物线的开口向下，其顶点即为最高点.
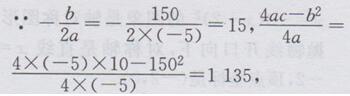
∴抛物线的顶点坐标为（15,1135）.
∴当t=15时，h最大值=1135.
答：经过15s，火箭达到它的最高点，最高点的高度为1135m.
习题2.5第4题答案
解：（1）当0≤x≤13时,学生的接受能力逐渐增强；当13≤x≤30时,学生的接受能力逐渐降低.
（2）有（1）知经过13min，学生的接受能力最强.
习题2.5第5题答案
解：∵左面抛物线的表达式为
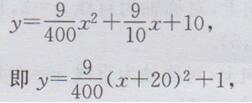
又∵右面抛物线的抛物线和左面抛物线的抛物线关于y轴对称，
∴右面抛物线的抛物线的对称轴为直线x=20，形状、开口方向等都不变.
∴右面抛物线的表达式应为
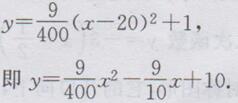
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
人教版九年级上册英语作业本答案江西省
浙教版九年级下册数学课本答案
九年级下册思想品德课课练答案苏人版
数学九年级下册学习与评价答案苏科版
苏人版九年级上册思想品德伴你学答案
九年级上册物理同步练习答案苏科版
北师大版九年级下册数学书答案
九年级下册数学作业本答案浙教版