第九章复习题第8题答案
解：在平行四边形ABCD中，∠D=∠B.
因为AB∥DF,所以∠BAE=∠F=62°．
因为AB =BE，所以∠BAE=∠BEA=62°.
所以∠B=180°-∠BAE-∠BEA=56°，
所以∠D=∠B=56°.
第九章复习题第9题答案
解：四边形ABD1C1是平行四边形．
证明如下：
因为△ABC和△D1B1C1都是等边三角形，
所以B1D1=AC，AB=C1 D1，∠D1B1C1=∠ACB=60°，
所以∠BB1D1=∠C1CA=120°，
又BB1 =C1C，
所以△BD1B1≌△C1AC．
所以BD1 =AC1．
又因为AB=C1D1，
所以四边形ABD1C1是平行四边形．
第九章复习题第10题答案
证明：
因为四边形ABCD是菱形，∠B=60°，
所以△ABC和△ACD都是等边三角形
所以∠B=∠FAC=60°，BC=AC，∠ACB=60°.
又因为BE=AF，
所以△BCE≌△ACF.
所以CE=CF．∠BCE=∠ACF.
所以∠ACB =∠BCE+ ∠ACE=∠ACF+∠ACE=∠ECF，即∠ECF=60°.
所以△ECF是等边三角形.
第九章复习题第11题答案
证明：
(1)∵四边形ABCD是平行四边形，
∴BC=AD，BC∥AD
∵H、F分别是AD、BC的中点，
∴AH= 1/2AD，FC=1/2BC，
∴AH= FC，AH∥FC，
∴四边形AFCH是平行四边形．
(2)∵四边形AFCH是平行四边形，
∴AF∥CH，∴AM//CN.
同理AN∥CM．
∴四边形AMCN是平行四边形.
(3)连接BD.在△ABD中，
∵E.H分别是AB、AD的中点，
∴EH=1/2BD，EH∥BD，
同理FG=1/2BD．FG∥BD，
∴EH=FG，EH//FG，
∴四边形EFGH是平行四边形.
第九章复习题第12题答案
解：(1)四边形ADEF是平行四边形
证明如下：
∵D、E分别是AB、BC的中点，
∴DE∥AC，DE=1/2AC.
∵F是AC的中点，
∴AF=1/2AC，
∴DE=AF，DE∥AF，
∴四边形ADEF是平行四边形.
(2)四边形ADEF是矩形．
证明如下：
由(1)知四边形ADEF是平行四边形
又∵∠A=90°，
∴平行四边形ADEF是矩形.
(3)四边形ADEF是菱形
证明如下：
∵DE=1/2AC,EF=1/2AB,AB=AC．
∴DE=EF.
由(1)知四边形ADEF是平行四边形，
∴平行四边形ADEF是菱形.
(4)四边形ADEF是正方形.
证明如下：
由(3)知四边形ADEF是菱形
又∵∠A=90°，
∴四边形ADEF是正方形.
第九章复习题第13题答案
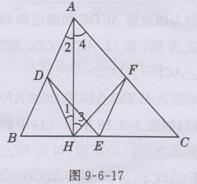
证明：如图9- 6-17.
∵AH⊥BC于点H，D为AB的中点，
∴DH=1/2 AB=AD，
∴∠1=∠2.
同理可证：∠3=∠4，
∴∠1+∠3=∠2+∠4，即∠DHF =∠DAF.
∵E、F分别为BC、AC的中点，
∴EF∥AB且EF=1/2AB,即EF∥AD且EF=AD,
∴四边形ADEF是平行四边形，
∴ ∠DAF=∠DEF,
∴∠DHF=∠DEF.
第九章复习题第14题答案
解：(1)22个平方单位；(2)本题答案不唯一，按要求设计并计算即可
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级上册数学配套练习册答案人教版
人教版八年级下册生物知识与能力训练答案
生物八年级上册学习与评价答案苏教版
八年级下册数学新课程自主学习与测评答案人教版
苏科版八年级上册生物伴你学答案
八年级上册生物学法大视野答案苏教版
八年级下册英语同步解析与测评答案人教版
八年级上册语文学法大视野答案人教版
八年级下册地理同步导学与优化训练答案人教版
八年级下册历史同步精练答案人教版