习题1.3第1题答案
解：（1）tan45度-sin30°=1-1/2=1/2 .
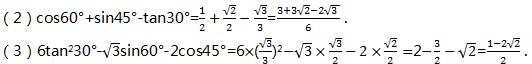
习题1.3第2题答案
解：如图1-2-7所示，
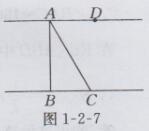
在Rt△ABC中，tan60°=AB/BC，
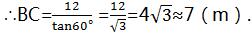
答：B、C之间的距离约为7米。
习题1.3第3题答案
解：在等腰△SAB中，∠ASB=120°，
∵SO⊥AB，∴∠ASO=1/2∠ASB=60° .
∵AB=54，∴AO=1/2AB=27 .
在Rt△ASO中，tan60°=AO/SO，
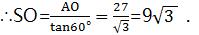
习题1.3第4题答案
解：如图1-2-10所示，
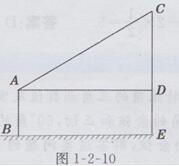
在Rt△ADC中，CD=AD∙tan∠CAD=5tan30°=5×/3=(5)/3(m)，
∴CE=CD+DE=(5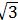
)/3+1.75≈4.6（m）.
答：这棵树大约4.6米高。
习题1.3第5题答案
解：∵AE⊥CD于点E，BF⊥CD于点F，
∴AE//BF .
又∵AB//CD，
∴四边形ABFE为平行四边形 。
∵∠AEF=90°，
∴四边形ABEF为矩形，
即AB=EF,且DE=CF.
在△BCF中，∵∠CBF = 45°，BF=0.8m，
∴CF=BFtan45°=0.8（m）
∴CD=DE+EF+FC=2.8（m）
∴四边形ABCD的面积S=1/2（AB+CD）∙AE =1/2×（1.2+2.8）×0.8=1.6（m2），则该段水渠最多能蓄水1.6×1500=2400（m3）.
习题1.3第6题答案
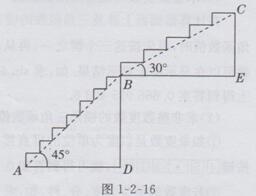
解：如图1-2-16所示，由楼梯的特性可知每个台阶的水平线与AD和BE都是平行的。它的铅直线都与BD和CE平行，若设AB部分有n1个台阶，BC部分有n2个台阶，则有方程n1×0.2+n2×0.2=BD+CE，即为（n1+n2）×0.2=BD+CE .
在Rt△ABD中，
∵∠A=45°，AD=1.5m，
∴BD=AD=1.5m，AB=AD/(cos45°)=3/（2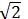
）（m）.
在Rt△BCE中，
∵∠B=30°，
∴CE=1/2BC=3/（4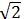
）（m），
∴（n1+n2）×0.2=1.5+3/（4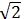
），
∴ n1+n2≈12.803 ，
∴n1+n2的值取13，即有13个台阶。
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册物理课时练答案人教版
苏科版九年级上册数学书答案
人教版九年级英语南方新课堂答案
人教版九年级上册语文新课程自主学习与测评答案
苏人版九年级上册思想品德伴你学答案
人教版九年级上册英语作业本答案
浙教版九年级上册数学书答案
九年级下册英语课课练答案译林版
九年级下册化学书答案鲁教版
九年级下册数学课时作业本答案人教版