第一章复习题第13题答案
解：此题答案不唯一.添加条件：∠CAB=∠DBA或∠CBA=∠DAB或AC=BD或BC=AD.选择添加条件AC=BD加以证明.
证明：在Rt△ACB和Rt△BDA中，
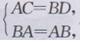
∴Rt△ACB≌Rt△BDA（HL）.
第一章复习题第14题答案
已知：在△ABC中，AB=AC,求证：∠B与∠C都是锐角.证明：∵AB=AC，∴∠B=∠C.假设∠B与∠C都为直角或钝角，于是∠B+∠C≥180°，这与三角形内角和定理矛盾，因此∠B和∠C必为锐角.即等腰三角形的底角必为锐角.
第一章复习题第15题答案
解：△AFD是直角三角形.理由如下：∵AB=AD，∴∠B=∠ADB=64°，∴△BAD=180°-∠ADB-∠B=180°-64°-64°=52°.∵∠BAC=72°，而∠BAC=∠BAD+∠DAC,∴∠DAC=∠BAC-∠BAD=72°-52°=20°.∵AD=DE, ∠E=55°，∴DAE=∠E=55°（等边对等角）.∵∠DAE=∠DAC+∠FAE,∴∠FAE=∠DAE-∠DAC=55°-20°=35°.∵∠AFD=∠FAE+∠E，∴∠AFD=35°+55°=90°，∴△AFD是直角三角形.
第一章复习题第16题答案
解：∵DE垂直平分AB，
∴AE=BE.
又∵BCE的周长=BE+EC+BC=AC+BC=8.
又∵AC-BC=2，得方程组
∵AB=AC ,
∴ AB=5.
第一章复习题第17题答案
证明：在等边三角形ABC中，AB=BC=AC，∠A=∠B=∠C.
∵AD=BE=CF,
∴ AB-AD=BC-BE=AC-CF，即DB=EC=FA.在△BDE和△CEF中，
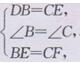
∴△BDE≌△CEF（SAS）.
∴ DE=EF.同理可证△AFD≌△CEF(SAS),
∴ FD=EF,DE=EF=FD.
∴△DEF是等边三角形.
第一章复习题第18题答案
解：作图如图1-5-30所示，△ABC是所求作的等腰直角三角形.
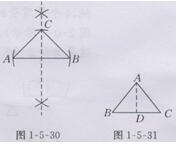
第一章复习题第19题答案
解：如图1-5-31所示,在等腰△ABC中,AB=AC=5，BC=6.过点A作AD⊥BC交BC于点D，
∴BD=1/2BC=3.
在Rt△ABD中，由勾股定理得AD2=AB2-BD2=52-32=16，
∴ AD=4.
∴S△ABC=1/2BC • AD=1/2×6×4=12.
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
人教版八年级下册历史知识与能力训练答案
八年级下册地理阳光学业评价答案人教版
八年级下册历史新课程自主学习与测评答案人教版
八年级下册历史与社会思想品德课时特训答案人教版
八年级下册思想品德新编基础训练答案人教版
人教版八年级上册英语长江作业本答案
语文八年级上册学习与评价答案苏教版
人教版八年级上册英语作业本答案